
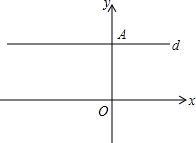
 如图,在平面直角坐标系中,点O为坐标原点,A(0,a),B(b,0),a与b为方程组$\left\{\begin{array}{l}{4a+3b=-11}\\{a+b=-5}\end{array}\right.$的解,过点A作x轴的平行线d
如图,在平面直角坐标系中,点O为坐标原点,A(0,a),B(b,0),a与b为方程组$\left\{\begin{array}{l}{4a+3b=-11}\\{a+b=-5}\end{array}\right.$的解,过点A作x轴的平行线d分析 (1)求出方程组中中a、b的值即可得出A、B两点的坐标;
(2)分0≤t<$\frac{9}{2}$与t≥$\frac{9}{2}$两种情况进行讨论;
(3)设R(-x,4),当0≤t≤4.5时,设P(9-2t,0),Q(0,4-4t),D(9-2t,4),则AQ=4t,PD=4,AR=-x,DR=9-2t+x,当△PRQ时以PQ为底的等腰直角三角形时可得出△ARQ≌△DPR,求出t的值;当t>4.5时,不存在以PQ为底的等腰直角三角形PRQ.
解答 解:(1)解方程组$\left\{\begin{array}{l}{4a+3b=-11}\\{a+b=-5}\end{array}\right.$得:$\left\{\begin{array}{l}{a=4}\\{b=-9}\end{array}\right.$,
则A的坐标是(0,4),B的坐标是(-9,0);
(2)当0≤t<$\frac{9}{2}$时,P在线段OB上,OP=9-2t,则S=$\frac{1}{2}$×4(9-2t),即S=-4t+18;
当t≥$\frac{9}{2}$时,P在BO的延长线上,OP=2t-9,则S=$\frac{1}{2}$×4(2t-9),即S=4t-18;
综上所述,S=$\left\{\begin{array}{l}18-4t(0≤t<4.5)\\ 4t-18(t≥4.5)\end{array}\right.$;
(3)如图所示,设R(-x,4),
当0≤t≤4.5时,设P(9-2t,0),Q(0,4-4t),D(9-2t,4),则AQ=4t,PD=4,AR=-x,DR=9-2t+x,当△PRQ时以PQ为底的等腰直角三角形时,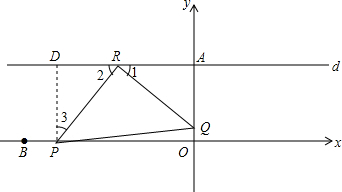
∵PR=QR,∠PRQ=90°,
∴∠1+∠2=∠2+∠3=90°,
∴∠1=∠3.
同理,∠2=∠AQR.
在△ARQ与△DPR中,
∵$\left\{\begin{array}{l}∠1=∠3\\ QR=PR\\∠AQR=∠2\end{array}\right.$,
∴△ARQ≌△DPR(ASA),
∴DP=AR,DR=AQ,即$\left\{\begin{array}{l}x=-4\\ 9-2t+x=4t\end{array}\right.$,解得t=$\frac{5}{6}$,
∴P(-$\frac{22}{3}$,0).
当t>4.5时,不存在以PQ为底的等腰直角三角形PRQ.
点评 本题考查的是一次函数综合题,涉及到一次函数图象上点的坐标特点及全等三角形的判定与性质等知识,在解答(2)(3)时要注意进行分类讨论.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
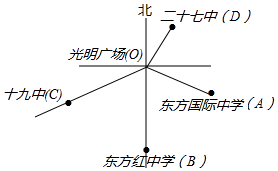 小明在光明广场(点O)绘制了市内几座学校相对广场的位置简图,(图中1cm表示5km),东方红中学在广场正南方向,测得OA=1.7cm,OB=2cm,OC=2cm,OD=1.4cm,∠AOC=123°18′,∠BOA=68°24′,∠AOD=88°28′,如何确定每个学校的具体位置?
小明在光明广场(点O)绘制了市内几座学校相对广场的位置简图,(图中1cm表示5km),东方红中学在广场正南方向,测得OA=1.7cm,OB=2cm,OC=2cm,OD=1.4cm,∠AOC=123°18′,∠BOA=68°24′,∠AOD=88°28′,如何确定每个学校的具体位置?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
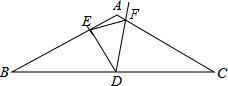 已知:△ABC中,AB=AC,∠BAC=120°,D为BC的中点,且∠EDF=∠C.
已知:△ABC中,AB=AC,∠BAC=120°,D为BC的中点,且∠EDF=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com