
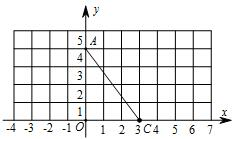
 如图,在平面直角坐标系中,A(0,4),C(3,0),
如图,在平面直角坐标系中,A(0,4),C(3,0),分析 (1)①如图1,画出线段AB,根据等腰三角形三线合一的性质得点B的坐标;
②如图2,证明△ACB≌△CAD(AAS),则AD=BC=6,得点D的坐标;
(2)先根据两组对边分别相等的四边形是平行四边形,证明四边形ABCD是平行四边形,根据平行四边形的性质:对角线互相平分得:E是AC的中点,根据中点坐标公式得出点E的坐标,由直线y=kx平分(1)中四边形ABCD的面积,可知:直线y=kx一定过点E,可求得k的值.
解答 解:(1)①如图1,点B的坐标为(-3,0);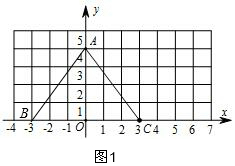
②如图2,∵A(0,4),C(3,0),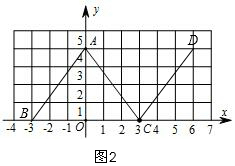
∴OA=4,OC=3,
由勾股定理得:AC=$\sqrt{{4}^{2}+{3}^{2}}$=5,
同理得:AB=5,
由旋转得:CD=AC=5,
∴AB=CD=AC,
∴∠ABC=∠ACB,∠CAD=∠ADC,
∵AD∥x轴,
∴∠CAD=∠ACB,
∴∠ABC=∠ADC,
∴△ACB≌△CAD(AAS),
∴AD=BC=6,
∴D(6,4);
(2)如图3,连接BD交AC于E,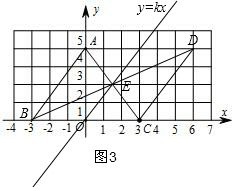
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AE=CE,
∵A(0,4),C(3,0),
∴E($\frac{3}{2}$,2),
∵直线y=kx平分(1)中四边形ABCD的面积,
∴直线y=kx过点E($\frac{3}{2}$,2),
把E($\frac{3}{2}$,2)代入y=kx中得:2=$\frac{3}{2}$k,
k=$\frac{4}{3}$.
点评 本题是一次函数的综合题,考查了对称、旋转的性质,平行四边形的性质和判定,利用待定系数法求正比例函数关系式,图形与坐标特点,熟练掌握轴对称的性质和坐标与图形特点是本题的关键,并注意数形结合的思想.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
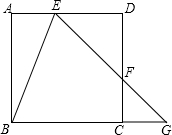 如图,正方形ABCD中,E,F分别在AD,DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;
如图,正方形ABCD中,E,F分别在AD,DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于4的整数个单位长度.
“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于4的整数个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
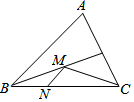 如图,在锐角三角形ABC中,BC=2,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值为$\sqrt{2}$.
如图,在锐角三角形ABC中,BC=2,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值为$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com