
【题目】已知购买1盆甲种花卉和3盆乙种花卉共需125元,购买3盆甲种花卉和2盆乙种花卉共需165元.
(1)求购买1盆甲种花卉和购买1盆乙种花卉各需多少元?
(2)某校为绿化校园决定购买甲乙两种花卉共60盆,要求购买的甲种花卉盆数不少于乙种花卉的 ![]() ,请帮该校设计一种最省钱的购买方案,并计算此时购买这两种花卉所需的费用.
,请帮该校设计一种最省钱的购买方案,并计算此时购买这两种花卉所需的费用.
【答案】
(1)解:设购买1盆甲种花卉要 x 元,购买1盆乙种花卉要 y 元,
![]() ,解得,
,解得, ![]() ,
,
答:购买1盆甲种花卉要35元,购买1盆乙种花卉30元
(2)解:设该校购买甲种花卉a盆,购买乙种花卉(60﹣a)盆,购买花卉的费用为w,
w=35a+30(60﹣a)=5a+1800,
∵购买的甲种花卉盆数不少于乙种花卉的 ![]() ,
,
∴a≥ ![]() (60﹣a),
(60﹣a),
解得,a≥12
∵a<60,
∴12≤a<60.
又∵5>0,
∴w随着a的增大而增大,
∴当a=12时,w最小,此时w=5×12+1800=1860,
∴当购买甲种花卉12盆、乙种花卉48盆时所需的费用最少,此时所购买这两种花卉所需的费用为1860元
【解析】(1)根据题意可以列出相应的二元一次方程组,从而可以解答本题;(2)根据题意可以得到费用与甲种花卉的函数关系式,然后根据购买的甲种花卉盆数不少于乙种花卉的 ![]() ,即可求得最省钱的购买方案,并计算此时购买这两种花卉所需的费用.
,即可求得最省钱的购买方案,并计算此时购买这两种花卉所需的费用.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】在平面内,分别用3根、5根、6根……火柴棒首尾依次相接,能搭成什么形状的三角形呢?通过尝试,列表如下.
火柴棒数 | 3 | 5 | 6 | … |
示意图 |
|
|
| … |
形状 | 等边三角形 | 等腰三角形 | 等边三角形 | … |
问:(1)4根火柴棒能搭成三角形吗?
(2)8根、12根火柴棒分别能搭成几种不同形状的三角形?并画出它们的示意图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
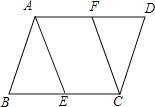
A. AF=CE B. AE=CF C. ∠BAE=∠FCD D. ∠BEA=∠FCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),四边形ABCD是平行四边形,BD是它的一条对角线,过顶点A、C分别作AM⊥BD,CN⊥BD,M,N为垂足. 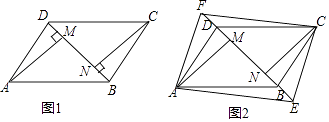
(1)求证:AM=CN;
(2)如图(2),在对角线DB的延长线及反向延长线上分别取点E,F,使BE=DF,连接AE、CF,试探究:当EF满足什么条件时,四边形AECF是矩形?并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两所学校共82人参加文艺汇演(其中甲校人数多于乙校人数,且甲校人数小于80人),如果两所学校分别购买服装,共付款6060元.
购买服装套数 | 1~40 | 41~80 | 81套及81套以上 |
每套服装价格 | 80元 | 70元 | 60元 |
(1)如果甲、乙两所学校联合起来购买服装,那么比各自购买服装一共可以节约多少钱?
(2)甲、乙两所学校各有多少学生参加演出?
(3)如果乙学校单独购买时,服装厂每件服装获利60%,丙学校购买的服装比乙多15套,那么服装厂卖给丙学校服装时共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】OB是∠AOC内部一条射线,OM是∠AOB平分线,ON是∠AOC平分线,OP是∠NOA平分线,OQ是∠MOA平分线,则∠POQ∶∠BOC=( )

A. 1∶2 B. 1∶3 C. 2∶5 D. 1∶4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上和有理数 a、b、c 对应的点的位置如图所示,有下面四个结论:①abc<0;②|a﹣b|+|b﹣c|=|a﹣c|③(a﹣b)(b﹣c)(c﹣a)>0;④|a|<1﹣bc,其中正确的结论有______.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com