
【题目】如图(1),四边形ABCD是平行四边形,BD是它的一条对角线,过顶点A、C分别作AM⊥BD,CN⊥BD,M,N为垂足. 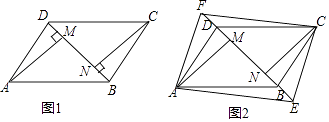
(1)求证:AM=CN;
(2)如图(2),在对角线DB的延长线及反向延长线上分别取点E,F,使BE=DF,连接AE、CF,试探究:当EF满足什么条件时,四边形AECF是矩形?并加以证明.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠ADM=∠CBN.
∵AM⊥BD,CN⊥BD,
∴∠AMD=∠CNB=90°,
在△AMD和△CNB中  ,
,
∴△AMD≌△CNB.
∴AM=CN.
(2)猜想:当EF=AC时,四边形AECF是矩形.
证明:由(1)得△AMD≌△CNB,
∴DM=BN.
∵BE=DF,
∴DM+DF=BN+BE,即MF=NE.
在△AMF和△CNE中 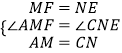
∴△AMF≌△CNE.
∴AF=CE,∠AFE=∠CEF.
∴AF∥CE且AF=CE.
即四边形AECF是平行四边形.
又EF=AC,
∴四边形AMCN是矩形
【解析】(1)利用平行四边形的性质证得△AMD≌△CNB,从而根据全等三角形对应边相等证得结论即可;(2)利用对角线相等的平行四边形是矩形证得结论即可.
【考点精析】通过灵活运用平行四边形的性质和矩形的判定方法,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形即可以解答此题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为检测某市正在销售的酸奶质量,应采用抽样调查的方式
B.两名同学连续六次的数学测试平均分相同,那么方差较大的同学的数学成绩更稳定
C.抛掷一个正方体骰子,点数为奇数的概率是 ![]()
D.“打开电视,正在播放动画片”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
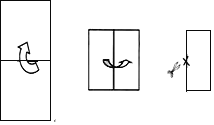
【题目】如图,将一个长为16,宽为8的矩形纸片先从下向上,再从左向右对折两次后,沿过所得矩形较长一边中点的直线剪掉一部分,再将剩下的打开,得到一个正方形,则这个正方形的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知购买1盆甲种花卉和3盆乙种花卉共需125元,购买3盆甲种花卉和2盆乙种花卉共需165元.
(1)求购买1盆甲种花卉和购买1盆乙种花卉各需多少元?
(2)某校为绿化校园决定购买甲乙两种花卉共60盆,要求购买的甲种花卉盆数不少于乙种花卉的 ![]() ,请帮该校设计一种最省钱的购买方案,并计算此时购买这两种花卉所需的费用.
,请帮该校设计一种最省钱的购买方案,并计算此时购买这两种花卉所需的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,抛物线y=﹣ ![]() x2+bx+c与x轴交于点A(﹣4,0),与y轴交于点B(0,4).
x2+bx+c与x轴交于点A(﹣4,0),与y轴交于点B(0,4).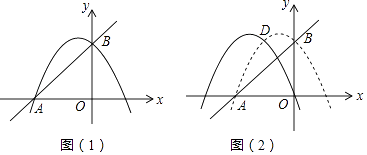
(1)求抛物线的函数解析式;
(2)在x轴上有一点P,点P在直线AB的垂线段为PC,C为垂足,且PC= ![]() ,求点P的坐标;
,求点P的坐标;
(3)如图(2),将原抛物线向左平移,使平移后的抛物线过原点,与原抛物线交于点D,在平移后的抛物线上是否存在点E,使S△APE=S△ACD?若存在,请求出点E的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公园有一条“Z”字形道路ABCD,其中AB∥CD,在E,M,F处各有一个小石凳,E、F分别在AB、CD上,且BE=CF,M为BC的中点,请问三个小石凳是否在一条直线上?说出你推断的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC. 
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)当四边形ABCD是形时,四边形OBEC是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com