
【题目】如图(1),在平面直角坐标系中,抛物线y=﹣ ![]() x2+bx+c与x轴交于点A(﹣4,0),与y轴交于点B(0,4).
x2+bx+c与x轴交于点A(﹣4,0),与y轴交于点B(0,4).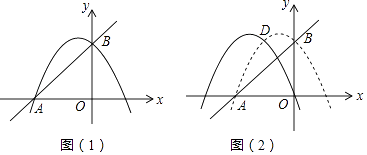
(1)求抛物线的函数解析式;
(2)在x轴上有一点P,点P在直线AB的垂线段为PC,C为垂足,且PC= ![]() ,求点P的坐标;
,求点P的坐标;
(3)如图(2),将原抛物线向左平移,使平移后的抛物线过原点,与原抛物线交于点D,在平移后的抛物线上是否存在点E,使S△APE=S△ACD?若存在,请求出点E的坐标,若不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=﹣ ![]() x2+bx+c过点A(﹣4,0),B(0,4),
x2+bx+c过点A(﹣4,0),B(0,4),
∴ ![]() ,解得:
,解得: ![]() ,
,
∴所求抛物线的函数解析式是y=﹣ ![]() x2﹣x+4
x2﹣x+4
(2)
解:∵A(﹣4,0),B(0,4),
∴OA=OB=4.
∵∠AOB=90°,
∴∠OAB=∠OBA=45°.
设PC⊥AB,则∠ACP=90°,PC= ![]() .
.

Rt△ACP中,sin∠PAC= ![]() ,
,
∴PA= ![]() =2.
=2.
∴OP=OA﹣PA=2或OP=OA+AP=6.
∴点P的坐标为:P1(﹣2,0),P2(﹣6,0)
(3)
解:∵抛物线y=﹣ ![]() x2﹣x+4向左平移后过原点,
x2﹣x+4向左平移后过原点,
∴平移后的抛物线的函数解析式为y=﹣ ![]() x2﹣3x.
x2﹣3x.
由﹣ ![]() x2﹣x+4=﹣
x2﹣x+4=﹣ ![]() x2﹣3x.
x2﹣3x.
解得 x=﹣2.
∴y=﹣ ![]() ×(﹣2)2﹣3×(﹣2)=4.
×(﹣2)2﹣3×(﹣2)=4.
∴点D的坐标为(﹣2,4).
如图2,①当点P在AO上时,设P1C1⊥AB,过C1作C1N⊥x轴,垂足为N,

在Rt△AC1P1中,∵∠C1AP1=45°,AP1=2,
∴AC1=P1C1= ![]() .
.
∴AN=NC1=1.
∴点C1的坐标为(﹣3,1).
∴ ![]() =
= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() ×2×4﹣
×2×4﹣ ![]() ×2×1﹣
×2×1﹣ ![]() ×4×1=4﹣1﹣2=1.
×4×1=4﹣1﹣2=1.
②当点P在OA延长线上时,同理可得点C2的坐标为(﹣5,﹣1). ![]() =1,
=1,
设点E(a,b),当S△APE=S△ACD时,有 ![]() ×2×|b|=1.即|﹣
×2×|b|=1.即|﹣ ![]() a2﹣3a|=1.
a2﹣3a|=1.
∴﹣ ![]() a2﹣3a=1或﹣
a2﹣3a=1或﹣ ![]() a2﹣3a=﹣1.
a2﹣3a=﹣1.
∴a1=﹣3+ ![]() ,a2=﹣3﹣
,a2=﹣3﹣ ![]() ,a3=﹣3+
,a3=﹣3+ ![]() ,a4=﹣3﹣
,a4=﹣3﹣ ![]() .
.
∴存在点E,使S△APE=S△ACD,点E的坐标为:(﹣3+ ![]() ,1)或(﹣3﹣
,1)或(﹣3﹣ ![]() ,﹣1)或(﹣3+
,﹣1)或(﹣3+ ![]() ,﹣1)或(﹣3﹣
,﹣1)或(﹣3﹣ ![]() ,﹣1)
,﹣1)
【解析】(1)由A、B两点的坐标可求得解析式;(2)由OA=OB=4知∠OAB=∠OBA=45°,根据sin∠PAC= ![]() 、PC=
、PC= ![]() 可得PA的长,从而由OP=OA﹣PA或OP=OA+AP得出答案;(3)由平移后的抛物线y=﹣
可得PA的长,从而由OP=OA﹣PA或OP=OA+AP得出答案;(3)由平移后的抛物线y=﹣ ![]() x2﹣3x得出D(﹣2,4),分点P在AO上和点P在OA延长线上利用割补法求得△ACD的面积为1,设点E(a,b),根据S△APE=S△ACD得
x2﹣3x得出D(﹣2,4),分点P在AO上和点P在OA延长线上利用割补法求得△ACD的面积为1,设点E(a,b),根据S△APE=S△ACD得 ![]() ×2×|b|=1.即|﹣
×2×|b|=1.即|﹣ ![]() a2﹣3a|=1,解方程即可得出答案.
a2﹣3a|=1,解方程即可得出答案.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为半圆上一动点,过点C作⊙O的切线l的垂线BD,垂足为D,BD与⊙O交于点E,连接OC,CE,AE,AE交OC于点F. 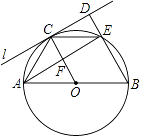
(1)求证:△CDE≌△EFC;
(2)若AB=4,连接AC. ①当AC=时,四边形OBEC为菱形;
②当AC=时,四边形EDCF为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某容器由A、B、C三个连通长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是整个容器容积的![]() (容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(1)求注满整个容器所需的总时间;
(2)设容器A的高度为xcm,则容器B的高度为 cm;
(3)求容器A的高度和注水的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
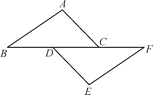
【题目】如图,点D,C在BF上,AC∥DE,∠A=∠E,BD=CF.
(1)求证:AB=EF;
(2)连接AF,BE,猜想四边形ABEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),四边形ABCD是平行四边形,BD是它的一条对角线,过顶点A、C分别作AM⊥BD,CN⊥BD,M,N为垂足. 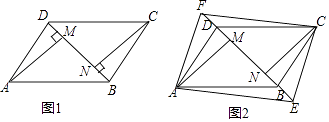
(1)求证:AM=CN;
(2)如图(2),在对角线DB的延长线及反向延长线上分别取点E,F,使BE=DF,连接AE、CF,试探究:当EF满足什么条件时,四边形AECF是矩形?并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知∠B和∠C的平分线相交于点F,经过点F作DE//BC,交AB于D,交AC于点E,若BD+CE=9,则线段DE的长为( )
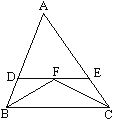
A. 9 B. 8 C. 7 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,![]() AOD=120
AOD=120![]() ,
, ![]() AOC=90
AOC=90![]() ,OE平分
,OE平分![]() BOD,则图中彼此互补的角共有( )
BOD,则图中彼此互补的角共有( )
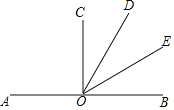
A. 4对 B. 5对 C. 6对 D. 7对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若一次函数![]() 的图象与x轴的交于点
的图象与x轴的交于点![]() ,与y轴交于点
,与y轴交于点![]() 下列结论:①关于x的方程
下列结论:①关于x的方程![]() 的解为
的解为![]() ;②
;②![]() 随x的增大而减小;③关于x的方程
随x的增大而减小;③关于x的方程![]() 的解为
的解为![]() ;④关于x的不等式
;④关于x的不等式![]() 的解为
的解为![]() 其中所有正确的为
其中所有正确的为![]()
![]()

A. ①②③ B. ①③ C. ①②④ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com