
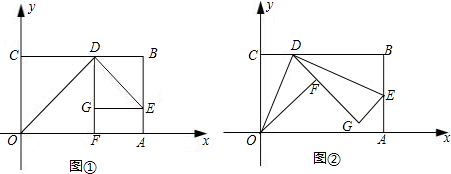
平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6),D是BC边上的动点(与点B、C不重合).如图②,将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,将△BDE沿DE翻折,得到△GDE,并使直线DG,DF重合.
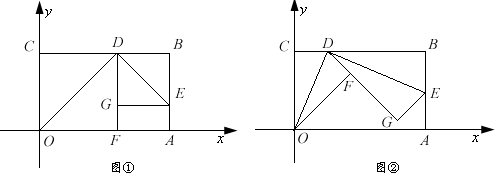
(1)图①中,若△COD翻折后点F落在OA边上,求直线DE的解析式.
(2)设(1)中所求直线DE与x轴交于点M,请你猜想过点M、C且关于y轴对称的抛物线与直线DE的公共点的个数,在图①的图形中,通过计算验证你的猜想.
(3)图②中,设E(10,b),求b的最小值.
|
(1)据题意可知:D(6,6),E(10,2) 1分 设直线DE的解析式y=kx+b 则 ∴直线DE的解析式:y=-x+12 2分 (2)直线DE的解析式:y=-x+12 令y=0,得x=12,∴M(12,0) 设过点M(12,0)、C(0,6)且关于y轴对称的抛物线为:y=ax2+c 可求 猜想:直线DE∶y=-x+12与抛物线: 证明:直线DE∶y=-x+12代入抛物线: 化简得:x2-24x+144=0 ∴ ∴直线DE:y=-x+12与抛物线: (3)设E(10,b),D(m,6)据题意可知: ∠OCD=∠DBE=90°,∠CDO=∠FDO,∠BDE=∠GDE ∵∠CDO+∠FDO+∠BDE+∠GDE=180° ∴∠CDO+∠BDE=90° ∵∠COD+∠CDO=90° ∴∠COD=∠BDE ∴△COD∽△BDE 6分 ∴ 据题意,可知:BE=6-b,BD=10-m, |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
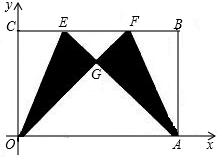 (1)求m的值;
(1)求m的值;查看答案和解析>>
科目:初中数学 来源: 题型:
 形BEFG是否存在邻边相等的情况?若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由.
形BEFG是否存在邻边相等的情况?若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
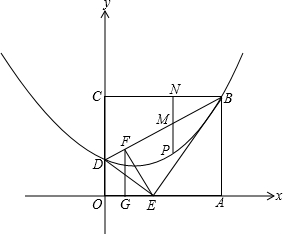
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com