
【题目】先化简,再求值: ![]() ﹣
﹣ ![]() ÷(1﹣
÷(1﹣ ![]() ).其中m满足一元二次方程m2+(5
).其中m满足一元二次方程m2+(5 ![]() tan30°)m﹣12cos60°=0.
tan30°)m﹣12cos60°=0.
【答案】解:原式= ![]() ﹣
﹣ ![]() ÷
÷ ![]() =
= ![]() ﹣
﹣ ![]()
![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() =
= ![]() ,
,
方程m2+(5 ![]() tan30°)m﹣12cos60°=0,化简得:m2+5m﹣6=0,
tan30°)m﹣12cos60°=0,化简得:m2+5m﹣6=0,
解得:m=1(舍去)或m=﹣6,
当m=﹣6时,原式=﹣ ![]() .
.
【解析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到最简结果,求出m的值代入计算即可求出值.
【考点精析】根据题目的已知条件,利用分式的混合运算的相关知识可以得到问题的答案,需要掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]}.


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16.
(1)求C点坐标;
(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.
(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F等于( ) 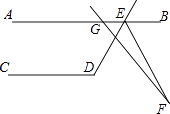
A.9.5°
B.19°
C.15°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )

A. 6 B. 5 C. 4 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.

(1)∵DE∥AB,( 已知 )
∴∠2= . ( , )
(2)∵DE∥AB,(已知 )
∴∠3= .( , )
(3)∵DE∥AB(已知 ),
∴∠1+ =180°.( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线.
(1)如图1,若AD=BD,求∠A的度数;
(2)如图2,在(1)的条件下,作DE⊥AB于E,连接EC.求证:△EBC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板按如图所示的方式摆放,其中△ABC为含有45°角的三角板,直线AD是等腰直角三角板的对称轴,且斜边上的点D为另一块三角板DMN的直角顶点,DM、DN分别交AB、AC于点E、F.则下列四个结论:①BD=AD=CD;②△AED≌△CFD;③BE+CF=EF;④S四边形AEDF=![]() BC2.其中正确结论是_____(填序号).
BC2.其中正确结论是_____(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
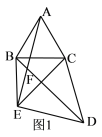
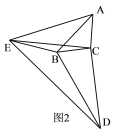
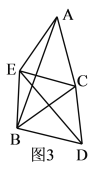
【题目】如图已知△CAB和△CDE中,CA=CB,CD=CE,∠BCA=∠DCE=![]() .连BE,BD.
.连BE,BD.
(1)如图1,若∠BCA=60![]() ,BD与AE交于点F,求∠AFB的度数;
,BD与AE交于点F,求∠AFB的度数;
(2)如图2,请探究∠EBD,∠AEB与![]() 之间的关系;
之间的关系;
(3)如图3,直接写出∠EBD,∠AEB与![]() 之间的关系.
之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 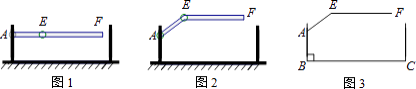
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com