
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 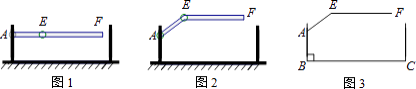
A.
B.
C.
D.
【答案】A
【解析】解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H, 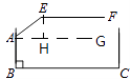
则∠EHG=∠HEF=90°,
∵∠AEF=143°,
∴∠AEH=∠AEF﹣∠HEF=53°,
∠EAH=37°,
在△EAH中,∠EHA=90°,∠EAH=37°,AE=1.2米,
∴EH=AEsin∠EAH≈1.2×0.60=0.72(米),
∵AB=1.2米,
∴AB+EH≈1.2+0.72=1.92≈1.9米.
故选:A.
过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.先求出∠AEH=53°,则∠EAH=37°,然后在△EAH中,利用正弦函数的定义得出EH=AEsin∠EAH,则栏杆EF段距离地面的高度为:AB+EH,代入数值计算即可.


 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】【阅读理解】
我们知道,当a>0且b>0时,( ![]() ﹣
﹣ ![]() )2≥0,所以a﹣2
)2≥0,所以a﹣2 ![]() +≥0,从而a+b≥2
+≥0,从而a+b≥2 ![]() (当a=b时取等号),
(当a=b时取等号),
【获得结论】设函数y=x+ ![]() (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x= ![]() 即x=
即x= ![]() 时,函数y有最小值为2
时,函数y有最小值为2 ![]()
(1)【直接应用】
若y1=x(x>0)与y2= ![]() (x>0),则当x=时,y1+y2取得最小值为 .
(x>0),则当x=时,y1+y2取得最小值为 .
(2)【变形应用】
若y1=x+1(x>﹣1)与y2=(x+1)2+4(x>﹣1),则 ![]() 的最小值是
的最小值是
(3)【探索应用】
在平面直角坐标系中,点A(﹣3,0),点B(0,﹣2),点P是函数y= ![]() 在第一象限内图象上的一个动点,过P点作PC⊥x轴于点C,PD⊥y轴于点D,设点P的横坐标为x,四边形ABCD的面积为S
在第一象限内图象上的一个动点,过P点作PC⊥x轴于点C,PD⊥y轴于点D,设点P的横坐标为x,四边形ABCD的面积为S
①求S与x之间的函数关系式;
②求S的最小值,判断取得最小值时的四边形ABCD的形状,并说明理由.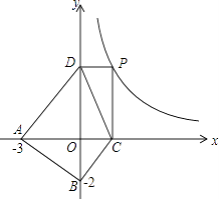
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照如下步骤计算:6﹣2÷( ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ).
).
(1)计算:( ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )÷6﹣2;
)÷6﹣2;
(2)根据两个算式的关系,直接写出6﹣2÷( ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )的结果.
)的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,直角边AC=7cm,BC=3cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F. 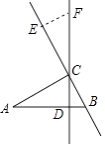
(1)求证:∠A=∠BCD;
(2)点E运动多长时间,CF=AB?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,按学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题: 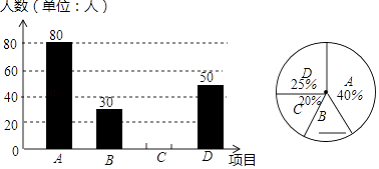
(1)本次共调查了名学生;
(2)在扇形统计图中,“B”所在扇形的圆心角是度;
(3)将条形统计图补充完整;
(4)若该中学有1200名学生,喜欢篮球运动的学生约有名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com