
ЁОЬтФПЁПЁОдФЖСРэНтЁП
ЮвУЧжЊЕРЃЌЕБaЃО0ЧвbЃО0ЪБЃЌЃЈ ![]() Љ
Љ ![]() ЃЉ2Ён0ЃЌЫљвдaЉ2
ЃЉ2Ён0ЃЌЫљвдaЉ2 ![]() +Ён0ЃЌДгЖјa+bЁн2
+Ён0ЃЌДгЖјa+bЁн2 ![]() ЃЈЕБa=bЪБШЁЕШКХЃЉЃЌ
ЃЈЕБa=bЪБШЁЕШКХЃЉЃЌ
ЁОЛёЕУНсТлЁПЩшКЏЪ§y=x+ ![]() ЃЈaЃО0ЃЌxЃО0ЃЉЃЌгЩЩЯЪіНсТлПЩжЊЃКЕБx=
ЃЈaЃО0ЃЌxЃО0ЃЉЃЌгЩЩЯЪіНсТлПЩжЊЃКЕБx= ![]() МДx=
МДx= ![]() ЪБЃЌКЏЪ§yгазюаЁжЕЮЊ2
ЪБЃЌКЏЪ§yгазюаЁжЕЮЊ2 ![]()
ЃЈ1ЃЉЁОжБНггІгУЁП
Шєy1=xЃЈxЃО0ЃЉгыy2= ![]() ЃЈxЃО0ЃЉЃЌдђЕБx=ЪБЃЌy1+y2ШЁЕУзюаЁжЕЮЊ ЃЎ
ЃЈxЃО0ЃЉЃЌдђЕБx=ЪБЃЌy1+y2ШЁЕУзюаЁжЕЮЊ ЃЎ
ЃЈ2ЃЉЁОБфаЮгІгУЁП
Шєy1=x+1ЃЈxЃОЉ1ЃЉгыy2=ЃЈx+1ЃЉ2+4ЃЈxЃОЉ1ЃЉЃЌдђ ![]() ЕФзюаЁжЕЪЧ
ЕФзюаЁжЕЪЧ
ЃЈ3ЃЉЁОЬНЫїгІгУЁП
дкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЈЉ3ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌЉ2ЃЉЃЌЕуPЪЧКЏЪ§y= ![]() дкЕквЛЯѓЯоФкЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌЙ§PЕузїPCЁЭxжсгкЕуCЃЌPDЁЭyжсгкЕуDЃЌЩшЕуPЕФКсзјБъЮЊxЃЌЫФБпаЮABCDЕФУцЛ§ЮЊS
дкЕквЛЯѓЯоФкЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌЙ§PЕузїPCЁЭxжсгкЕуCЃЌPDЁЭyжсгкЕуDЃЌЩшЕуPЕФКсзјБъЮЊxЃЌЫФБпаЮABCDЕФУцЛ§ЮЊS
ЂйЧѓSгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкЧѓSЕФзюаЁжЕЃЌХаЖЯШЁЕУзюаЁжЕЪБЕФЫФБпаЮABCDЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ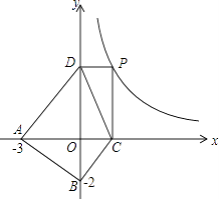
ЁОД№АИЁП
ЃЈ1ЃЉ1ЃЛ2
ЃЈ2ЃЉ4
ЃЈ3ЃЉ
НтЃКЂйЩшPЃЈxЃЌ ![]() ЃЉЃЌдђCЃЈxЃЌ0ЃЉЃЌDЃЈ0ЃЌ
ЃЉЃЌдђCЃЈxЃЌ0ЃЉЃЌDЃЈ0ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрAC=x+3ЃЌBD= ![]() +2ЃЌ
+2ЃЌ
ЁрS= ![]() ACBD=
ACBD= ![]() ЃЈx+3ЃЉЃЈ
ЃЈx+3ЃЉЃЈ ![]() +2ЃЉ=6+x+
+2ЃЉ=6+x+ ![]() ЃЛ
ЃЛ
ЂкЁпxЃО0ЃЌ
Ёрx+ ![]() Ён2
Ён2 ![]() =6ЃЌ
=6ЃЌ
ЁрЕБx= ![]() ЪБЃЌМДx=3ЪБЃЌx+
ЪБЃЌМДx=3ЪБЃЌx+ ![]() газюаЁжЕ6ЃЌ
газюаЁжЕ6ЃЌ
ЁрДЫЪБS=6+x+ ![]() газюаЁжЕ12ЃЌ
газюаЁжЕ12ЃЌ
Ёпx=3ЃЌ
ЁрPЃЈ3ЃЌ2ЃЉЃЌCЃЈ3ЃЌ0ЃЉЃЌDЃЈ0ЃЌ2ЃЉЃЌ
ЁрAЁЂCЙигкxжсЖдГЦЃЌDЁЂBЙигкyжсЖдГЦЃЌМДЫФБпаЮABCDЕФЖдНЧЯпЛЅЯрДЙжБЦНЗжЃЌ
ЁрЫФБпаЮABCDЮЊСтаЮЃЎ
ЁОНтЮіЁПНтЃКЃЈ1ЃЉЁпxЃО0ЃЌЁрy1+y2=x+ ![]() Ён2
Ён2 ![]() =2ЃЌЁрЕБx=
=2ЃЌЁрЕБx= ![]() ЪБЃЌМДx=1ЪБЃЌy1+y2газюаЁжЕ2ЃЌЫљвдД№АИЪЧЃК1ЃЛ2ЃЛЃЈ2ЃЉЁпxЃОЉ1ЃЌЁрx+1ЃО0ЃЌЁр
ЪБЃЌМДx=1ЪБЃЌy1+y2газюаЁжЕ2ЃЌЫљвдД№АИЪЧЃК1ЃЛ2ЃЛЃЈ2ЃЉЁпxЃОЉ1ЃЌЁрx+1ЃО0ЃЌЁр ![]() =
= ![]() =ЃЈx+1ЃЉ+
=ЃЈx+1ЃЉ+ ![]() Ён2
Ён2 ![]() =4ЃЌЁрЕБx+1=
=4ЃЌЁрЕБx+1= ![]() ЪБЃЌМДx=1ЪБЃЌ
ЪБЃЌМДx=1ЪБЃЌ ![]() газюаЁжЕ4ЃЌЫљвдД№АИЪЧЃК4ЃЛ
газюаЁжЕ4ЃЌЫљвдД№АИЪЧЃК4ЃЛ
ЁОПМЕуОЋЮіЁПБОЬтжївЊПМВщСЫЗДБШР§КЏЪ§ЕФаджЪЕФЯрЙижЊЪЖЕуЃЌашвЊеЦЮеаджЪ:ЕБkЃО0ЪБЫЋЧњЯпЕФСНжЇЗжБ№ЮЛгкЕквЛЁЂЕкШ§ЯѓЯоЃЌдкУПИіЯѓЯоФкyжЕЫцxжЕЕФдіДѓЖјМѕаЁЃЛ ЕБkЃМ0ЪБЫЋЧњЯпЕФСНжЇЗжБ№ЮЛгкЕкЖўЁЂЕкЫФЯѓЯоЃЌдкУПИіЯѓЯоФкyжЕЫцxжЕЕФдіДѓЖјдіДѓВХФме§ШЗНтД№ДЫЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
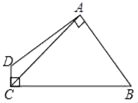
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBAC=90ЁуЃЌAB=ACЃЌADЪЧОЙ§AЕуЕФвЛЬѕжБЯпЃЌЧвBЁЂCдкADЕФСНВрЃЌBDЁЭADгкDЃЌCEЁЭADгкEЃЌНЛABгкЕуFЃЌCE=10ЃЌBD=4ЃЌдђDEЕФГЄЮЊЃЈЁЁЁЁЃЉ

A. 6 B. 5 C. 4 D. 8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
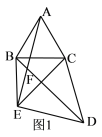
ЁОЬтФПЁПШчЭМвбжЊЁїCABКЭЁїCDEжаЃЌCA=CBЃЌCD=CEЃЌЁЯBCA=ЁЯDCE=![]() .СЌBEЃЌBD.
.СЌBEЃЌBD.
ЃЈ1ЃЉШчЭМ1ЃЌШєЁЯBCA=60![]() ЃЌBDгыAEНЛгкЕуFЃЌЧѓЁЯAFBЕФЖШЪ§ЃЛ
ЃЌBDгыAEНЛгкЕуFЃЌЧѓЁЯAFBЕФЖШЪ§ЃЛ
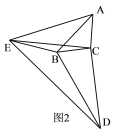
ЃЈ2ЃЉШчЭМ2ЃЌЧыЬНОПЁЯEBDЃЌЁЯAEBгы![]() жЎМфЕФЙиЯЕЃЛ
жЎМфЕФЙиЯЕЃЛ
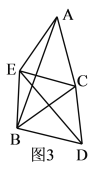
ЃЈ3ЃЉШчЭМ3ЃЌжБНгаДГіЁЯEBDЃЌЁЯAEBгы![]() жЎМфЕФЙиЯЕ.
жЎМфЕФЙиЯЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌAC=6![]() ЃЌBD=6ЃЌEЪЧBCБпЕФжаЕуЃЌPЃЌMЗжБ№ЪЧACЃЌABЩЯЕФЖЏЕуЃЌСЌНгPEЃЌPMЃЌдђPE+PMЕФзюаЁжЕЪЧЃЈЁЁЁЁЃЉ
ЃЌBD=6ЃЌEЪЧBCБпЕФжаЕуЃЌPЃЌMЗжБ№ЪЧACЃЌABЩЯЕФЖЏЕуЃЌСЌНгPEЃЌPMЃЌдђPE+PMЕФзюаЁжЕЪЧЃЈЁЁЁЁЃЉ

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌABЃНADЃЌACЃН5ЃЌЁЯDABЃНЁЯDCBЃН90ЁуЃЌдђЫФБпаЮABCDЕФУцЛ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉдЫгУЭъШЋЦНЗНЙЋЪНМЦЫуЃК992
ЃЈ2ЃЉЯШЛЏМђЃЌдйЧѓжЕЃКЃЈ2x+3yЃЉ2ЉЃЈ2x+yЃЉЃЈ2xЉyЃЉЃЌЦфжа xЃН![]() ЃЌyЃН
ЃЌyЃН![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕиЯТГЕПтГіПкДІАВзАСЫЁАСНЖЮЪНРИИЫЁБЃЌШчЭМ1ЫљЪОЃЌЕуAЪЧРИИЫзЊЖЏЕФжЇЕуЃЌЕуEЪЧРИИЫСНЖЮЕФСЊНсЕуЃЎЕБГЕСООЙ§ЪБЃЌРИИЫAEFзюЖржЛФмЩ§Ц№ЕНШчЭМ2ЫљЪОЕФЮЛжУЃЌЦфЪОвтЭМШчЭМ3ЫљЪОЃЈРИИЫПэЖШКіТдВЛМЦЃЉЃЌЦфжаABЁЭBCЃЌEFЁЮBCЃЌЁЯAEF=143ЁуЃЌAB=AE=1.2УзЃЌФЧУДЪЪКЯИУЕиЯТГЕПтЕФГЕСОЯоИпБъжОХЦЮЊЃЈ ЃЉЃЈВЮПМЪ§ОнЃКsin37ЁуЁж0.60ЃЌcos37ЁуЁж0.80ЃЌtan37ЁуЁж0.75ЃЉ 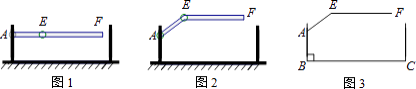
A.
B.
C.
D.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
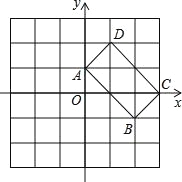
ЁОЬтФПЁПШчЭМЃЌдк 6ЁС6 ЕФЭјИёжаЃЌЫФБпаЮ ABCD ЕФЖЅЕуЖМдкИёЕуЩЯЃЌУПИіИёзгЖМЪЧБпГЄЮЊ 1 ЕФе§ЗНаЮЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЎ
ЃЈ1ЃЉЛГіЫФБпаЮ ABCD Йигк y жсЖдГЦКЭЫФБпаЮ AЁфBЁфCЁфDЁфЃЈЕу AЁЂBЁЂCЁЂDЕФЖдГЦЕуЗжБ№ЪЧЕу AЁфBЁфCЁфDЁфЃЎ
ЃЈ2ЃЉЧѓ AЁЂBЁфЁЂBЁЂC ЫФЕузщГЩКЭЫФБпаЮЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪааТНЈЛ№ГЕеОЙуГЁНЋЭЖШыЪЙгУЃЌМЦЛЎдкЙуГЁФкжжжВAЃЌBСНжжЛЈФОЙВ4000ПУЃЌШєAЛЈФОЪ§СПЪЧBЛЈФОЪ§СПЕФ2БЖЛЙЖр400ПУЃЎ
ЃЈ1ЃЉЧѓAЃЌBСНжжЛЈФОЕФЪ§СПЗжБ№ЪЧЖрЩйПУЃП
ЃЈ2ЃЉШчЙћдАСжДІАВХХ24ШЫЭЌЪБжжжВетСНжжЛЈФОЃЌУПШЫУПЬьФмжжжВAЛЈФО70ПУЛђBЛЈФО60ПУЃЌгІдѕбљЗжБ№АВХХжжжВAЛЈФОКЭжжжВBЛЈФОЕФШЫЪ§ЃЌВХФмШЗБЃЭЌЪБЭъГЩИїздЕФШЮЮёЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com