
【题目】如图,半径OA=2cm,圆心角为90°的扇形OAB中,C为 ![]() 的中点,D为OB的中点,则图中阴影部分的面积为cm2 .
的中点,D为OB的中点,则图中阴影部分的面积为cm2 . 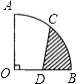
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F等于( ) 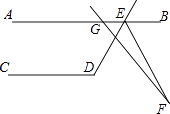
A.9.5°
B.19°
C.15°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板按如图所示的方式摆放,其中△ABC为含有45°角的三角板,直线AD是等腰直角三角板的对称轴,且斜边上的点D为另一块三角板DMN的直角顶点,DM、DN分别交AB、AC于点E、F.则下列四个结论:①BD=AD=CD;②△AED≌△CFD;③BE+CF=EF;④S四边形AEDF=![]() BC2.其中正确结论是_____(填序号).
BC2.其中正确结论是_____(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
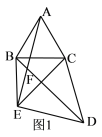
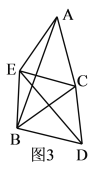
【题目】如图已知△CAB和△CDE中,CA=CB,CD=CE,∠BCA=∠DCE=![]() .连BE,BD.
.连BE,BD.
(1)如图1,若∠BCA=60![]() ,BD与AE交于点F,求∠AFB的度数;
,BD与AE交于点F,求∠AFB的度数;
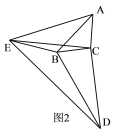
(2)如图2,请探究∠EBD,∠AEB与![]() 之间的关系;
之间的关系;
(3)如图3,直接写出∠EBD,∠AEB与![]() 之间的关系.
之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD与EF相交.
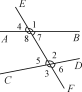
(1)图中∠1和∠2分别在直线AB,CD的同_______,并且都在直线EF的_____,具有这样位置关系的一对角叫做______;
(2)图中∠2和∠8都在直线AB,CD____,并且分别在直线EF的___,具有这样位置关系的一对角叫做_____;
(3)图中∠2和∠7都在直线AB,CD____,且都在直线EF的____,具有这样位置关系的一对角叫做______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 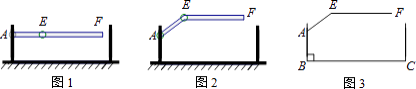
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠C=90°时,测得AC=2 ![]() ,当∠C=120°时,如图2,AC=( )
,当∠C=120°时,如图2,AC=( ) 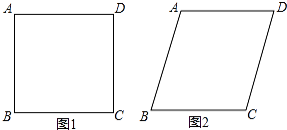
A.2
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com