
【题目】已知△ABC在正方形网格中的位置如图所示,则点P是△ABC的( ) 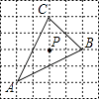
A.外心
B.内心
C.三条高线的交点
D.三条中线的交点
【答案】D
【解析】解:A、三角形的外心是三角形的三条垂直平分线的交点,故错误; B、三角形的内心是三角形的三条角平分线的交点,故错误;
C、三条高线的交点为三角形的垂心,故错误;
D、三角形的重心是三角形的三条中线的交点,故正确;
故选D.
【考点精析】利用三角形的“三线”和勾股定理的概念对题目进行判断即可得到答案,需要熟知1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.

(1)∵DE∥AB,( 已知 )
∴∠2= . ( , )
(2)∵DE∥AB,(已知 )
∴∠3= .( , )
(3)∵DE∥AB(已知 ),
∴∠1+ =180°.( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD与EF相交.
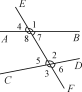
(1)图中∠1和∠2分别在直线AB,CD的同_______,并且都在直线EF的_____,具有这样位置关系的一对角叫做______;
(2)图中∠2和∠8都在直线AB,CD____,并且分别在直线EF的___,具有这样位置关系的一对角叫做_____;
(3)图中∠2和∠7都在直线AB,CD____,且都在直线EF的____,具有这样位置关系的一对角叫做______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC、CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.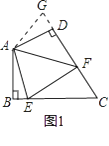
(1)小明同学探究此问题的方法是,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;
(2)探索延伸:
如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF= ![]() ∠BAD,上述结论是否仍然成立,请说明理由;
∠BAD,上述结论是否仍然成立,请说明理由; 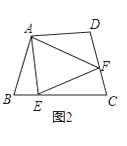
(3)实际应用:
如图③,在某次军事演习中,舰艇甲在指挥中心O北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,当∠EOF=70°时,两舰艇之间的距离是海里.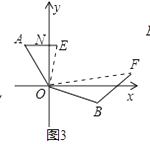
(4)能力提高:
如图④,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为 . 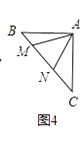
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 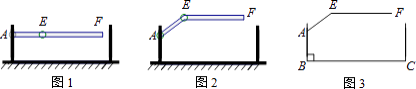
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点F是线段AC上一点,点E是线段BC上一点,BF与AE交于点H,∠BAE=∠FBC,AG⊥BF,∠GAF:∠BEA=1:10,则∠BAE=_____°.
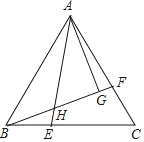
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com