
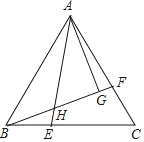
【题目】在等边三角形ABC中,点F是线段AC上一点,点E是线段BC上一点,BF与AE交于点H,∠BAE=∠FBC,AG⊥BF,∠GAF:∠BEA=1:10,则∠BAE=_____°.
【答案】20
【解析】
由△ABE≌△BCF(ASA),推出∠AEB=∠BFC,由题意可以假设∠GAF=x,则∠AEB=∠BFC=10x,由∠AGF=90°,可得∠GAF+∠AFG=90°,由此构建方程求出x即可解决问题.
∵△ABC是等边三角形,
∴AB=BC,∠ABE=∠C=60°,
∵∠BAE=∠FBC,
∴△ABE≌△BCF(ASA),
∴∠AEB=∠BFC,
∵∠GAF:∠BEA=1:10,
∴可以假设:∠GAF=x,则∠AEB=∠BFC=10x,
∵AG⊥BF,
∴∠AGF=90°,
∴∠GAF+∠AFG=90°,
∴x+(180°-10x)=90°,
∴x=10°,
∴∠AEB=100°,
∴∠BAE=180°-60°-100°=20°,
故答案为20.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是CD上一点,DF⊥BE交BE的延长线于点G,交BC的延长线于点F. 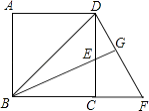
(1)求证:△BCE≌△DCF.
(2)若∠DBE=∠CBE,求证:BD=BF.
(3)在(2)的条件下,求CE:ED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,E为AD的中点,F为BC边上一动点,设BF=t(0≤t≤2),线段EF的垂直平分线GH分别交边CD,AB于点G,H,过E做EM⊥BC于点M,过G作GN⊥AB于点N. 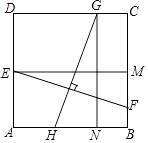
(1)当t≠2时,求证:△EMF≌△GNH;
(2)顺次连接E、H、F、G,设四边形EHFG的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_____,A,B两点间的距离是_____;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是_____,A,B两点间的距离为_____;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_____,A、B两点间的距离是_____;
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示什么数?A,B两点间的距离为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC。
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com