
【题目】如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC。
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC。

【答案】(1)证明见解析;(2)50°
【解析】
(1)首先连接AC,根据AM⊥CD,AN⊥BC,判断出AM、AN分别是CD、BC的垂直平分线,得到AC=AD,AB=AC,再根据等腰三角形三线合一的性质得到∠DAM=∠CAM,∠BAN=∠CAN,然后根据角的和差即可得出结论;
(2)由∠MAN=70°,得出∠BAD的度数.由四边形ANCM内角和等于360°,得到∠BCD的度数.在△BCD中,由三角形内角和定理得到∠BDC的度数.在△ABD中,根据等腰三角形的性质和三角形内角和定理可得出∠ADB的度数,根据角的和差即可得出结论.
(1)如图,连接AC.
∵M、N分别是CD、BC的中点,且AM⊥CD,AN⊥BC,∴AM、AN分别是CD、BC的垂直平分线,∴AC=AD,AB=AC.
∵AM⊥CD,AN⊥BC,∴∠DAM=∠CAM,∠BAN=∠CAN,∴∠DAC+∠BAC=2∠CAM+2∠CAN,∴∠BAD=2∠MAN;
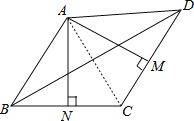
(2)∵∠MAN=70°,∴∠BAD=2∠MAN=140°.
∵AM⊥CD,AN⊥BC,∴∠BCD=180°-∠MAN=180°-70°=110°.
∵∠DBC=40°,∴∠BDC=180°-∠DBC-∠BCD=180°-40°-110°=30°.
∵AB=AC=AD,∴∠ABD=∠ADB.
∵∠BAD=140°,∴∠ABD=∠ADB=20°,∴∠ADC=∠ADB+∠BDC=20°+30°=50°.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
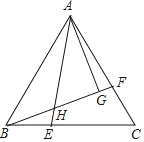
【题目】在等边三角形ABC中,点F是线段AC上一点,点E是线段BC上一点,BF与AE交于点H,∠BAE=∠FBC,AG⊥BF,∠GAF:∠BEA=1:10,则∠BAE=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
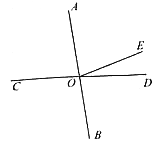
【题目】如图,AB、CD交于点O,∠AOE=4∠DOE,∠AOE的余角比∠DOE小10°(题中所说的角均是小于平角的角).
(1)求∠AOE的度数;
(2)请写出∠AOC在图中的所有补角;
(3)从点O向直线AB的右侧引出一条射线OP,当∠COP=∠AOE+∠DOP时,求∠BOP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ![]() ≈1.7)
≈1.7) 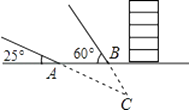
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC. 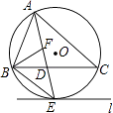
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( ) 
A.当行驶速度为40km/h时,每消耗1升汽油,甲车能行驶20km
B.消耗1升汽油,丙车最多可行驶5km
C.当行驶速度为80km/h时,每消耗1升汽油,乙车和丙车行驶的最大公里数相同
D.当行驶速度为60km/h时,若行驶相同的路程,丙车消耗的汽油最少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 若|a|=﹣a,则 a 一 定是负数
B. 单项式 x3y2z 的系数为 1,次数是 6
C. 若 AP=BP,则点 P 是线段 AB 的中点
D. 若∠AOC=![]() ∠AOB,则射线 OC 是∠AOB 的平分线
∠AOB,则射线 OC 是∠AOB 的平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的角平分线上一点,过P作PC//OA交OB于点C.若∠AOB=30°,OC=4cm,则点P到OA的距离PD等于___________cm.
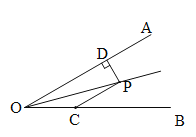
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com