
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC. 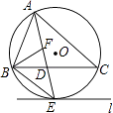
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
【答案】
(1)解:直线l与⊙O相切.
理由:如图1所示:连接OE、OB、OC.
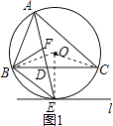
∵AE平分∠BAC,
∴∠BAE=∠CAE.
∴ ![]() .
.
∴∠BOE=∠COE.
又∵OB=OC,
∴OE⊥BC.
∵l∥BC,
∴OE⊥l.
∴直线l与⊙O相切.
(2)解:∵BF平分∠ABC,
∴∠ABF=∠CBF.
又∵∠CBE=∠CAE=∠BAE,
∴∠CBE+∠CBF=∠BAE+∠ABF.
又∵∠EFB=∠BAE+∠ABF,
∴∠EBF=∠EFB.
∴BE=EF.
(3)解:由(2)得BE=EF=DE+DF=7.
∵∠DBE=∠BAE,∠DEB=∠BEA,
∴△BED∽△AEB.
∴ ![]() ,即
,即 ![]() ,解得;AE=
,解得;AE= ![]() .
.
∴AF=AE﹣EF= ![]() ﹣7=
﹣7= ![]() .
.
【解析】(1)连接OE、OB、OC.由题意可证明 ![]() ,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;(2)先由角平分线的定义可知∠ABF=∠CBF,然后再证明∠CBE=∠BAF,于是可得到∠EBF=∠EFB,最后依据等角对等边证明BE=EF即可;(3)先求得BE的长,然后证明△BED∽△AEB,由相似三角形的性质可求得AE的长,于是可得到AF的长.
,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;(2)先由角平分线的定义可知∠ABF=∠CBF,然后再证明∠CBE=∠BAF,于是可得到∠EBF=∠EFB,最后依据等角对等边证明BE=EF即可;(3)先求得BE的长,然后证明△BED∽△AEB,由相似三角形的性质可求得AE的长,于是可得到AF的长.


科目:初中数学 来源: 题型:
【题目】如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( ) 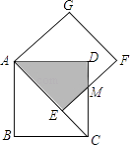
A.﹣4+4 ![]()
B.4 ![]() +4
+4
C.8﹣4 ![]()
D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两种饮料,这两种饮料的体积和单价如表:
类型 | A | B |
单瓶饮料体积/升 | 1 | 2.5 |
单价/元 | 3 | 4 |
(1)小明购买A、B两种饮料共13升,用了25元,他购买A,B两种饮料个各多少瓶?
(2)若购买A、B两种饮料共36瓶,且A种饮料的数量不多于B种饮料的数量,则最少可以购买多少升饮料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC。
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)当PN∥BC时,判断△ACP的形状,并说明理由;
(2)点P在滑动时,当AP长为多少时,△ADP与△BPC全等,为什么?
(3)点P在滑动时,△PCD的形状可以是等腰三角形吗?若可以,请求出夹角α的大小;若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:2017年3月在北京市召开的第十二届全国人民代表大会第五次会议上,环境问题再次成为大家议论的重点内容之一. 北京自1984年开展大气监测,至2012年底,全市已建立监测站点35个.2013年,北京发布的首个PM2.5年均浓度值为89.5微克/立方米.2014年,北京空气中的二氧化硫年均浓度值达到了国家新的空气质量标准;二氧化氮、PM10、PM2.5年均浓度值超标,其中PM2.5年均浓度值为85.9微克/立方米.2016年,北京空气中的二氧化硫年均浓度值远优于国家标准;二氧化氮、PM10、PM2.5的年均浓度值分别为48微克/立方米、92微克/立方米、73微克/立方米.与2015年相比,二氧化硫、二氧化氮、PM10年均浓度值分别下降28.6%、4.0%、9.8%;PM2.5年均浓度值比2015年的年均浓度值80.6微克/立方米有较明显改善.(以上数据来源于北京市环保局)
根据以上材料解答下列问题:
(1)2015年北京市二氧化氮年均浓度值为微克/立方米;
(2)请你用折线统计图将2013﹣2016年北京市PM2.5的年均浓度值表示出来,并在图上标明相应的数据.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com