
����Ŀ�����ⱳ����
��ͼ�٣����ı���ABCD�У�AB=AD����BAD=120�㣬��B=��ADC=90�㣬E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF=60�㣮̽��ͼ���߶�BE��EF��FD֮���������ϵ��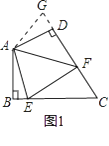
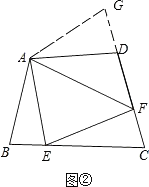
��1��С��ͬѧ̽��������ķ����ǣ��ӳ�FD����G��ʹDG=BE������AG����֤����ABE��ADG����֤����AEF�ա�AGF���ɵó����ۣ����Ľ���Ӧ����
��2��̽�����죺
��ͼ�ڣ������ı���ABCD�У�AB=AD����B+��D=180�㣮E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF= ![]() ��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
��BAD�����������Ƿ���Ȼ��������˵�����ɣ� 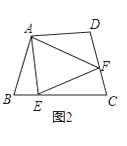
��3��ʵ��Ӧ�ã�
��ͼ�ۣ���ij�ξ�����ϰ�У���ͧ����ָ������O��ƫ��30���A������ͧ����ָ��������ƫ��70���B������������ͧ��ָ�����ĵľ�����ȣ��ӵ��ж�ָ���ͧ��������������60����/Сʱ���ٶ�ǰ������ͧ���ر�ƫ��50��ķ�����80����/Сʱ���ٶ�ǰ����2Сʱ��ָ�����Ĺ۲�ס�������ͧ�ֱ�E��F��������EOF=70��ʱ������֮ͧ��ľ��������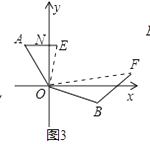
��4��������ߣ�
��ͼ�ܣ�����ֱ��������ABC�У���BAC=90�㣬AB=AC����M��N�ڱ�BC�ϣ��ҡ�MAN=45�㣮��BM=1��CN=3����MN�ij�Ϊ �� 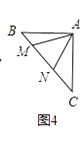
���𰸡�
��1��EF=BE+DF
��2��
�⣺����EF=BE+DF��Ȼ������
���ɣ��ӳ�FD����G��ʹDG=BE������AG����ͼ�ڣ�
�ڡ�ABE�͡�ADG�У� 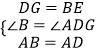 ��
��
���ABE�ա�ADG��SAS����
��AE=AG����BAE=��DAG��
�ߡ�EAF= ![]() ��BAD��
��BAD��
���GAF=��DAG+��DAF=��BAE+��DAF=��BAD����EAF=��EAF��
���EAF=��GAF��
�ڡ�AEF�͡�GAF�У� 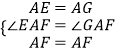 ��
��
���AEF�ա�AGF��SAS����
��EF=FG��
��FG=DG+DF=BE+DF��
��EF=BE+DF��
��3��280
��4��![]()
���������⣺��1.��EF=BE+DF��֤�����£�
�ڡ�ABE�͡�ADG�У� 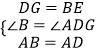 ��
��
���ABE�ա�ADG��SAS����
��AE=AG����BAE=��DAG��
�ߡ�EAF= ![]() ��BAD��
��BAD��
���GAF=��DAG+��DAF=��BAE+��DAF=��BAD����EAF=��EAF��
���EAF=��GAF��
�ڡ�AEF�͡�GAF�У� 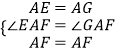 ��
��
���AEF�ա�AGF��SAS����
��EF=FG��
��FG=DG+DF=BE+DF��
��EF=BE+DF��
���Դ��� EF=BE+DF��
��3.����ͼ�ۣ�����EF���ӳ�AE��BF�ཻ�ڵ�C��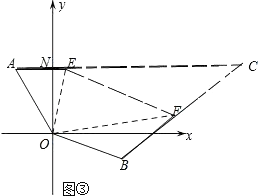
�ߡ�AOB=30��+90��+��90�㩁70�㣩=140�㣬��EOF=70�㣬
���EOF= ![]() ��AOB��
��AOB��
�֡�OA=OB����OAC+��OBC=��90�㩁30�㣩+��70��+50�㣩=180�㣬
�����̽�������е�������
�����EF=AE+BF������
��EF=2����60+80��=280���
�𣺴�ʱ����֮ͧ��ľ�����280���
���Դ��ǣ�280��
��4.����ͼ4��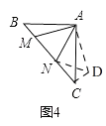
����ABM�Ƶ�A��ʱ����ת�õ���ACD��
���ABM�ա�ACD��
���AMB=��ADC����BAM=��CAM��AM=AD��BM=CD=1��
�ߡ�AMB+��AMC=90�㣬
���AMC+��ADC=180�㣬
���MAD+��MCD=180�㣬
�ߡ�BAC=90�㣬
���MAD=��MAC+��CAD=��MAC+��BAM=90�㣬
���MCD=90�㣬
��Rt��NCD��CN=3��CD=1��
���ݹ��ɶ����ã�ND= ![]() ��
��
�ߡ�MAD=90�㣬��MAN=45�㣬
���DAN=45�㣬
��AM=AD��AN=AN��
���MAN�ա�DAN��
��MN=DN= ![]() ��
��
���Դ��� ![]() ��
��
�����㾫�����������⣬������Ҫ�˽�ȫ�������ε�����(ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ�����)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���������ABC���Ե�AΪԲ�ģ�ACΪ�뾶������BC���ڵ�E���ֱ��Ե�E��CΪԲ�ģ��Դ��� ![]() EC�ij�Ϊ�뾶�����ཻ�ڵ�P��������AP����BC�ڵ�D����BC=5��AD=4��tan��BAD=
EC�ij�Ϊ�뾶�����ཻ�ڵ�P��������AP����BC�ڵ�D����BC=5��AD=4��tan��BAD= ![]() ����AC�ij�Ϊ�� ��
����AC�ij��� �� 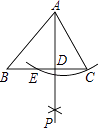
A.3
B.5
C.![]()
D.2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A(a��0)��B(b��0)����![]() +| b-6|=0.
+| b-6|=0.
��1����A��B�����ꣻ
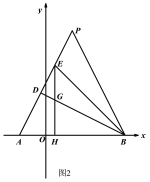
��2����ͼ2����PΪAB�Ĵ�ֱƽ������һ�㣬BD��AP�ڵ�D��BE����PBD�Ľ�ƽ������EH��AB�ڵ�H����BD�ڵ�G����AD=m��DE=n������BEG��������ú�m��n��ʽ�ӱ�ʾ����
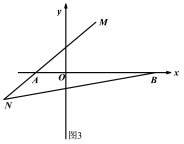
��3����ͼ3����M��AB�Ĵ�ֱƽ�����ϣ�����MAB=40������N��MA���ӳ����ϣ���MN=8������ABN�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���������������У���������ÿ�����̵ƴ������������ල�ڣ�����Ȱ��Ա��ţij�������������ĵ�һ��ʮ��·�ڣ��Դ���Ƶ���������ͳ�ƣ���������7��00��12��00�и�ʱ��δ���Ƶ�������������ͼ��ʾ���в�������ͳ��ͼ�������ͳ��ͼ����������⣺ 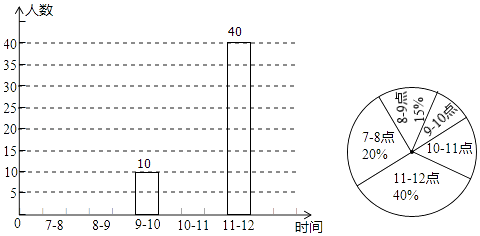
��1���ù�����7��00��12��00�����˴���ƣ�
��2���ٲ�ȫ����ͳ��ͼ�� �ڼ�������ͳ��ͼ��10��11������Ӧ��Բ�ĽǵĶ���.
��3���ù�����7��00��12��00����ʱ��δ���Ƶ������ķ�����
��4���������ͳ��ͼ�ṩ����Ϣ��ͨ�����������һ�����������飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
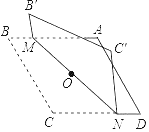
����Ŀ���Խ��߳��ֱ�Ϊ6��8������ABCD��ͼ��ʾ����OΪ�Խ��ߵĽ��㣬����O�۵����Σ�ʹB��B�������غϣ�MN���ۺۣ���B'M=1����CN�ij�Ϊ____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�������������е�λ����ͼ��ʾ�����P�ǡ�ABC�ģ� �� 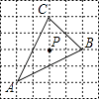
A.����
B.����
C.�������ߵĽ���
D.�������ߵĽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���BAD=��ADC=90�㣬AB=AD= ![]() ��CD=
��CD= ![]() ����P���ı���ABCD�ϣ���P��BD�ľ���Ϊ
����P���ı���ABCD�ϣ���P��BD�ľ���Ϊ ![]() �����P�ĸ���Ϊ�� ��
�����P�ĸ���Ϊ�� �� 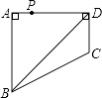
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC �У�AB��AC����BAC��120�㣬D Ϊ BC ���е㣬DE��AC �ڵ� E��AE��8���� CE �ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ4��������ABCD�У�EΪAD���е㣬FΪBC����һ���㣬��BF=t��0��t��2�����߶�EF�Ĵ�ֱƽ����GH�ֱ�CD��AB�ڵ�G��H����E��EM��BC�ڵ�M����G��GN��AB�ڵ�N�� 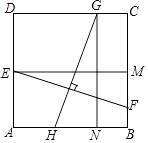
��1����t��2ʱ����֤����EMF�ա�GNH��
��2��˳������E��H��F��G�����ı���EHFG�����ΪS�����S���Ա���t֮��ĺ�����ϵʽ������S����Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com