
【题目】为创建国家文明城市,我市特在每个红绿灯处设置了文明监督岗,文明劝导员老牛某工作日在市中心的一个十字路口,对闯红灯的人数进行统计.根据上午7:00~12:00中各时间段闯红灯的人数制作了如图所示的尚不完整的统计图,请根据统计图解答下列问题: 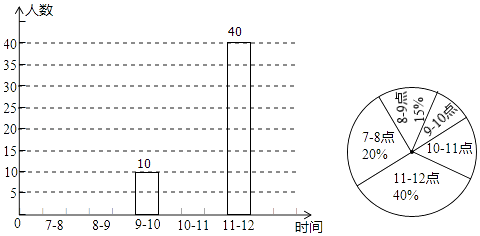
(1)该工作日7:00~12:00共有人闯红灯?
(2)①补全条形统计图, ②计算扇形统计图中10~11点所对应的圆心角的度数.
(3)该工作日7:00~12:00,各时间段闯红灯的人数的方差是
(4)请你根据统计图提供的信息向交通管理部门提出一条合理化建议.
【答案】
(1)100
(2)根据题意得:7﹣8点的人数为100×20%=20(人),8﹣9点的人数为100×15%=15(人),
9﹣10点所占的百分比是: ![]() ×100%=10%,10﹣11点占1﹣(20%+15%+10%+40%)=15%,人数为100×15%=15(人),补全图形,如图所示:
×100%=10%,10﹣11点占1﹣(20%+15%+10%+40%)=15%,人数为100×15%=15(人),补全图形,如图所示:
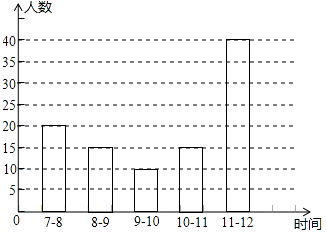
10~11点所对应的圆心角的度数为15%×360°=54°,故答案为:54°;
(3)110
(4)解:加强对11~12点时段的交通管理和交通安全教育.
【解析】解:(1.)根据题意得:40÷40%=100(人),则这一天上午7:00~12:00这一时间段共有100人闯红灯,所以答案是:100; (3.)根据题意得:各时间段闯红灯的人数的平均数是(20+15+10+15+40)÷5=20(人),则方差为 ![]() ×[(20﹣20)2+(15﹣20)2+(10﹣20)2+(15﹣20)2+(40﹣20)2]=110,所以答案是:110;
×[(20﹣20)2+(15﹣20)2+(10﹣20)2+(15﹣20)2+(40﹣20)2]=110,所以答案是:110;
【考点精析】解答此题的关键在于理解扇形统计图的相关知识,掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况,以及对条形统计图的理解,了解能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
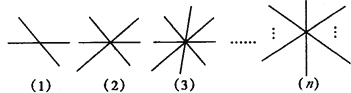
【题目】(1)两条直线相交于一点有2组不同的对顶角;
(2)三条直线相交于一点有6组不同的对顶角;
(3)四条直线相交于一点有12组不同的对顶角;
(4)n条直线相交于同一点有___________组不同对顶角.(如图所示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京奥运会开幕前,某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68 000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?(利润率=![]() ×100%)
×100%)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD与EF相交.
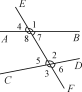
(1)图中∠1和∠2分别在直线AB,CD的同_______,并且都在直线EF的_____,具有这样位置关系的一对角叫做______;
(2)图中∠2和∠8都在直线AB,CD____,并且分别在直线EF的___,具有这样位置关系的一对角叫做_____;
(3)图中∠2和∠7都在直线AB,CD____,且都在直线EF的____,具有这样位置关系的一对角叫做______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+m(m>0)与x轴交于点A(-2,0),直线y=-x+n(n>0)与x轴、y轴分别交于B、C两点,并与直线y=2x+m(m>0)相交于点D,若AB=4.
(1)求点D的坐标;
(2)求出四边形AOCD的面积;
(3)若E为x轴上一点,且△ACE为等腰三角形,直接写出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC、CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.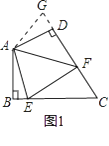
(1)小明同学探究此问题的方法是,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;
(2)探索延伸:
如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF= ![]() ∠BAD,上述结论是否仍然成立,请说明理由;
∠BAD,上述结论是否仍然成立,请说明理由; 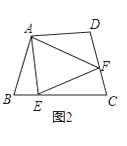
(3)实际应用:
如图③,在某次军事演习中,舰艇甲在指挥中心O北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,当∠EOF=70°时,两舰艇之间的距离是海里.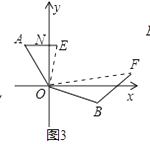
(4)能力提高:
如图④,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为 . 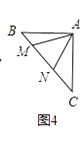
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目:初中数学 来源: 题型:
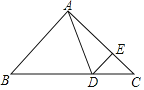
【题目】如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)当∠BAD=60°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com