
【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD= ![]() ,CD=
,CD= ![]() ,点P在四边形ABCD上,若P到BD的距离为
,点P在四边形ABCD上,若P到BD的距离为 ![]() ,则点P的个数为( )
,则点P的个数为( ) 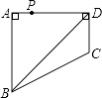
A.1
B.2
C.3
D.4
【答案】B
【解析】解:过点A作AE⊥BD于E,过点C作CF⊥BD于F, 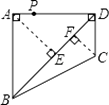
∵∠BAD=∠ADC=90°,AB=AD= ![]() ,CD=
,CD= ![]() ,
,
∴∠ABD=∠ADB=45°,
∴∠CDF=90°﹣∠ADB=45°,
∵sin∠ABD= ![]() ,
,
∴AE=ABsin∠ABD=2 ![]() sin45°
sin45°
=2 ![]()
![]() =2>
=2> ![]() ,
,
所以在AB和AD边上有符合P到BD的距离为 ![]() 的点2个,
的点2个,
∵sin∠CDF= ![]() ,
,
∴CF=CDsin∠CDF= ![]()
![]() =1<
=1< ![]() ,
,
所以在边BC和CD上没有到BD的距离为 ![]() 的点,
的点,
总之,P到BD的距离为 ![]() 的点有2个.
的点有2个.
故选:B.
【考点精析】解答此题的关键在于理解点到直线的距离的相关知识,掌握从直线外一点到这条直线的垂线段的长度叫做点到直线的距离,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+m(m>0)与x轴交于点A(-2,0),直线y=-x+n(n>0)与x轴、y轴分别交于B、C两点,并与直线y=2x+m(m>0)相交于点D,若AB=4.
(1)求点D的坐标;
(2)求出四边形AOCD的面积;
(3)若E为x轴上一点,且△ACE为等腰三角形,直接写出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC、CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.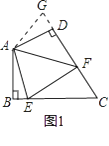
(1)小明同学探究此问题的方法是,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;
(2)探索延伸:
如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF= ![]() ∠BAD,上述结论是否仍然成立,请说明理由;
∠BAD,上述结论是否仍然成立,请说明理由; 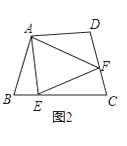
(3)实际应用:
如图③,在某次军事演习中,舰艇甲在指挥中心O北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,当∠EOF=70°时,两舰艇之间的距离是海里.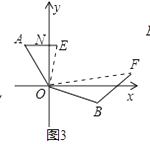
(4)能力提高:
如图④,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为 . 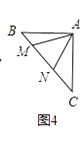
查看答案和解析>>
科目:初中数学 来源: 题型:
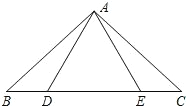
【题目】如图,点 D,E 在△ABC的边 BC上,连接AD,AE.下面有三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成以下三个命题:命题Ⅰ“如果①② 成立,那么③成立”; 命题Ⅱ“如果①③成立,那么②成立”;命题Ⅲ“如果②③成立,那么①成立”.
(1)以上三个命题是真命题的为__________(直接作答);
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小伟和小欣玩一种抽卡片游戏:将背面完全相同、正面分别写有1,2,3,4的四张卡片背面向上洗匀后,小伟和小欣各自随机抽取一张(不放回).将小伟的数字作为十位数字,小欣的数字作为个位数字,组成一个两位数.如果所组成的两位数为偶数,则小伟胜;否则小欣胜.
(1)当小伟抽取的卡片数字为2时,问两人谁获胜的可能性大?
(2)通过计算判断这个游戏对小伟和小欣是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
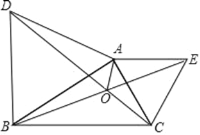
【题目】如图,分别以△ABC 的边 AB,AC 向外作等边三角形 ABD 和等边三角形 ACE,线段 BE 与 CD 相交于点 O,连接 OA.
(1)求证:BE=DC;
(2)求∠BOD 的度数;
(3)求证:OA 平分∠DOE.
(4)猜想线段 OA、OB、OD 的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com