
【题目】小伟和小欣玩一种抽卡片游戏:将背面完全相同、正面分别写有1,2,3,4的四张卡片背面向上洗匀后,小伟和小欣各自随机抽取一张(不放回).将小伟的数字作为十位数字,小欣的数字作为个位数字,组成一个两位数.如果所组成的两位数为偶数,则小伟胜;否则小欣胜.
(1)当小伟抽取的卡片数字为2时,问两人谁获胜的可能性大?
(2)通过计算判断这个游戏对小伟和小欣是否公平.
【答案】
(1)解:列表得:
数字 | 1 | 2 | 3 | 4 |
1 | ﹣﹣﹣ | 12 | 13 | 14 |
2 | 21 | ﹣﹣﹣ | 23 | 24 |
3 | 31 | 32 | ﹣﹣﹣ | 34 |
4 | 41 | 42 | 43 | ﹣﹣﹣ |
共有3种等可能的情况数,其中P(小伟胜)= ![]() ,P(小欣胜)=
,P(小欣胜)= ![]() ,
,
∴小欣获胜的可能性大.
(2)解:这个游戏对小伟和小欣是公平的.理由如下:
由(1)可知共有12种等可能结果,其中偶数占6个,奇数占6个,
∴P(小伟胜)= ![]() ,P(小欣胜)=
,P(小欣胜)= ![]() ,
,
∴这个游戏对小伟和小欣是公平的.
【解析】(1)找出十位数字为2的所有等可能的情况数,进而求出两人获胜的概率,比较即可得到结果;(2)这个游戏对小伟和小欣是公平的.根据题意,由(1)的图表,分别计算两人谁获胜的可能性,比较可得答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以进行这样的分解:n=p×q(p、q是正整数,且p≤q).如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并且规定F(n)=![]() .例如18=1×18=2×9=3×6,这时就有F(18)=
.例如18=1×18=2×9=3×6,这时就有F(18)=![]() .请解答下列问题:
.请解答下列问题:
(1)计算:F(24);
(2)当n为正整数时,求证:F(n3+2n2+n)=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
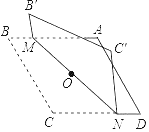
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD= ![]() ,CD=
,CD= ![]() ,点P在四边形ABCD上,若P到BD的距离为
,点P在四边形ABCD上,若P到BD的距离为 ![]() ,则点P的个数为( )
,则点P的个数为( ) 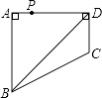
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形 ABC 中,∠A 的平分线交 BC 于点 D,过点 D 作 DE⊥AC, DF⊥AB,垂足分别为 E,F,下面四个结论:
①∠AFE=∠AEF;②AD 垂直平分 EF;③![]() ;④EF 一定平行 BC. 其中正确的是( )
;④EF 一定平行 BC. 其中正确的是( )
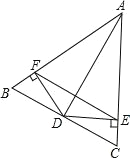
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
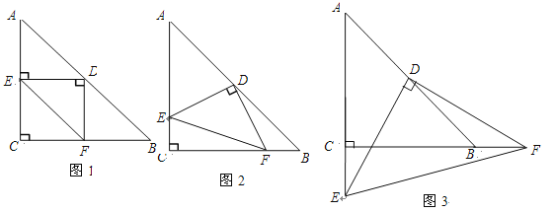
【题目】 已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F.当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证![]() .当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,
.当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,![]() ,
,![]() ,
,![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
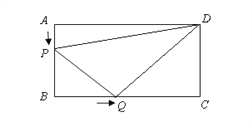
【题目】如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
(1)当PB=2厘米时,求点P移动多少秒?
(2)t为何值时,△PBQ为等腰直角三角形?
(3)求四边形PBQD的面积,并探究一个与计算结果有关的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com