
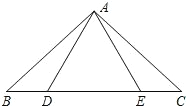
【题目】如图,点 D,E 在△ABC的边 BC上,连接AD,AE.下面有三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成以下三个命题:命题Ⅰ“如果①② 成立,那么③成立”; 命题Ⅱ“如果①③成立,那么②成立”;命题Ⅲ“如果②③成立,那么①成立”.
(1)以上三个命题是真命题的为__________(直接作答);
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D在边AC上,且
,D在边AC上,且![]() .
.
![]() 如图1,填空
如图1,填空![]() ______
______![]() ,
,![]() ______
______![]()
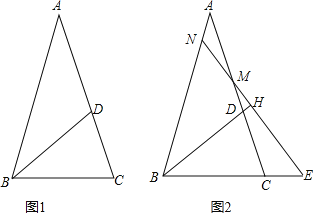
![]() 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线![]() 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知抛物线y=ax2+bx﹣3的对称轴为x=1,与x轴分别交于A、B两点,与y轴交于点C,一次函数y=x+1经过A,且与y轴交于点D.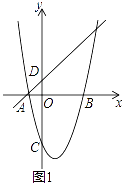
(1)求该抛物线的解析式.
(2)如图(2),点P为抛物线B、C两点间部分上的任意一点(不含B,C两点),设点P的横坐标为t,设四边形DCPB的面积为S,求出S与t的函数关系式,并确定t为何值时,S取最大值?最大值是多少?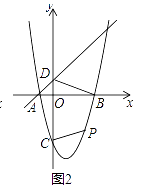
(3)如图(3),将△ODB沿直线y=x+1平移得到△O′D′B′,设O′B′与抛物线交于点E,连接ED′,若ED′恰好将△O′D′B′的面积分为1:2两部分,请直接写出此时平移的距离.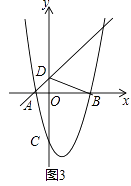
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为____.
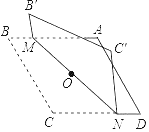
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD= ![]() ,CD=
,CD= ![]() ,点P在四边形ABCD上,若P到BD的距离为
,点P在四边形ABCD上,若P到BD的距离为 ![]() ,则点P的个数为( )
,则点P的个数为( ) 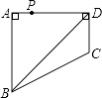
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
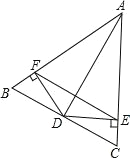
【题目】如图,三角形 ABC 中,∠A 的平分线交 BC 于点 D,过点 D 作 DE⊥AC, DF⊥AB,垂足分别为 E,F,下面四个结论:
①∠AFE=∠AEF;②AD 垂直平分 EF;③![]() ;④EF 一定平行 BC. 其中正确的是( )
;④EF 一定平行 BC. 其中正确的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
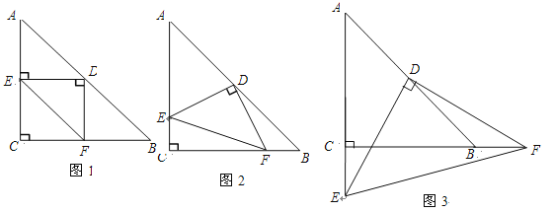
【题目】 已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F.当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证![]() .当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,
.当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,![]() ,
,![]() ,
,![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若AC = 8,CB = 6,求线段MN的长;
(2)若AC = a,MN = b,求线段BC的长用含![]() ,
,![]() 的代数式可以表示.
的代数式可以表示.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com