
【题目】观察下列图形:已知a∥b,在第一个图中,可得∠1+∠2=180°,则按照以上规律,∠1+∠2+∠P1+…+∠Pn=______度.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
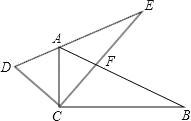
【题目】两个全等的三角尺重叠摆放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转到△DCE的位置,使点A恰好落在边DE上,AB与 CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=16cm,则AF=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D为AC边上的一点,DG∥AB,延长AB到E,使BE=GD,连接DE交BC于F.
(1)求证:GF=BF;
(2)若△ABC的边长为a,BE的长为b,且a,b满足(a﹣7)2+b2﹣6b+9=0,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于 ![]() EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=
EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD= ![]() ,则AC的长为( )
,则AC的长为( ) 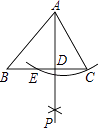
A.3
B.5
C.![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
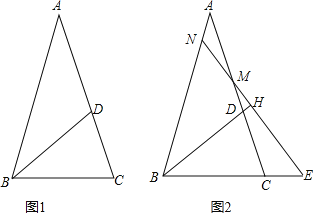
【题目】如图,在![]() 中,
中,![]() ,D在边AC上,且
,D在边AC上,且![]() .
.
![]() 如图1,填空
如图1,填空![]() ______
______![]() ,
,![]() ______
______![]()
![]() 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线![]() 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以进行这样的分解:n=p×q(p、q是正整数,且p≤q).如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并且规定F(n)=![]() .例如18=1×18=2×9=3×6,这时就有F(18)=
.例如18=1×18=2×9=3×6,这时就有F(18)=![]() .请解答下列问题:
.请解答下列问题:
(1)计算:F(24);
(2)当n为正整数时,求证:F(n3+2n2+n)=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
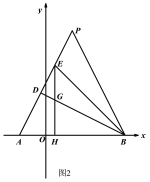
【题目】如图,在平面直角坐标系中,点A(a,0),B(b,0),且![]() +| b-6|=0.
+| b-6|=0.
(1)求A,B的坐标;
(2)如图2,点P为AB的垂直平分线上一点,BD⊥AP于点D,BE是△PBD的角平分线,EH⊥AB于点H,交BD于点G,若AD=m,DE=n,求△BEG的面积(用含m,n的式子表示);
(3)如图3,点M在AB的垂直平分线上,且∠MAB=40°,点N在MA的延长线上,且MN=8,求∠ABN的度数.

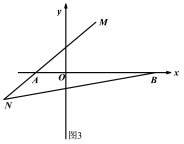
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD= ![]() ,CD=
,CD= ![]() ,点P在四边形ABCD上,若P到BD的距离为
,点P在四边形ABCD上,若P到BD的距离为 ![]() ,则点P的个数为( )
,则点P的个数为( ) 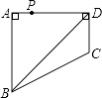
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com