
| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
分析 (1)根据众数和中位数的定义可得;
(2)先根据加权平均数求得训练后的人均进球数,再训练前的人均进球数为x,根据训练后的人均进球数比训练前增加25%,列方程求解可得.
解答 解:(1)由表格可知,4出现的次数最多,故众数为4,
中位数为$\frac{5+5}{2}$=5,
故答案为:4,5;
(2)训练后人均进球数为$\frac{8×2+7×1+6×4+5×7+4×8+3×2}{2+1+4+7+8+2}$=5,
设训练前的人均进球数为x,
则(1+25%)x=5,
解得:x=4,
答:训练前的人均进球数为4个.
点评 本题主要考查众数、中位数、平均数的计算和一元一次方程的应用,熟练掌握众数、中位数及加权平均数的计算公式和定义是解题的关键.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
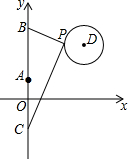 如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1-t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是$\sqrt{13}$-1.
如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1-t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是$\sqrt{13}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
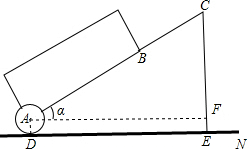 拉杆箱是人们出行的必需品,采用拉杆箱可以让我们的出行更轻松,如图,已知某种拉杆箱箱体长AB=50cm,拉杆最大伸长距离BC=40cm,点A到地面的距离AD=8cm,拉杆箱与水平面的夹角α的度数为35°.(提示:sin35°≈0.57,cos35°≈0.82).
拉杆箱是人们出行的必需品,采用拉杆箱可以让我们的出行更轻松,如图,已知某种拉杆箱箱体长AB=50cm,拉杆最大伸长距离BC=40cm,点A到地面的距离AD=8cm,拉杆箱与水平面的夹角α的度数为35°.(提示:sin35°≈0.57,cos35°≈0.82).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com