
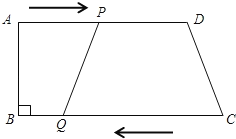
����Ŀ����ͼ��ʾ��������ABCD�У�AD��BC����B=90�㣬AD=24cm��BC=26cm������P�ӵ�A������AD�������D��1cm/s���ٶ��˶�������Q�ӵ�C��ʼ����CB�������B��3cm/s���ٶ��˶�����P��Q�ֱ�ӵ�A�͵�Cͬʱ������������һ�㵽��˵�ʱ����һ����ֹ֮ͣ�˶���
��1�������ʱ�䣬�ı���PQCD��ƽ���ı��Σ�
��2�������ʱ�䣬�ı���PQBA�Ǿ��Σ�
��3�������ʱ�䣬��PQ��ƽ����CDʱ����PQ=CD��

���𰸡���1��6�룻��2��6.5�룻��3��7��.
����������������1���辭��tsʱ���ı���PQCD��ƽ���ı��Σ�����DP=CQ�������������ɣ�
��2���辭��tsʱ���ı���PQBA�Ǿ��Σ�����AP=BQ�������������ɣ�
��3���辭��t��s�����ı���PQCD�ǵ������Σ�����EP=2�г��й�t�ķ�����⼴�ɣ�
��⣺��1���辭��x�룬�ı���PQCDΪƽ���ı���
��PD=CQ
����24��x=3x��
��ã�x=6��
��2���辭��y�룬�ı���PQBAΪ���Σ�
��AP=BQ��
����y=26��3y��
��ã�y=![]() ��
��
��3���辭��t�룬�ı���PQCD�ǵ������Σ�
��P����PE��AD����D����DF��BC��
���QEP=��DFC=90��
���ı���PQCD�ǵ������Σ�
��PQ=DC��
�֡�AD��BC����B=90�㣬
��AB=PE=DF��
��Rt��EQP��Rt��FCD��
PQ=DC
PE=DF
��Rt��EQP��Rt��FCD��HL����
��EQ=FC
��FC=BC��AD=26��24=2��
�֡�BQ=BC-CQ=26��3t��
��EQ=AP��BQ=t����26��3t��=4t-26��
��4t-26=2
�ã�t=7��
�ྭ��7s��PQ=CD��


 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E�ڱ�BC����CE=1����Ϊ![]() ���߶�MN��AC���˶������ı���BMNE���ܳ���Сʱ����tan��MBC��ֵ�� ��
���߶�MN��AC���˶������ı���BMNE���ܳ���Сʱ����tan��MBC��ֵ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�BFƽ����ABC��AD�ڵ�F��AE��BF�ڵ�O����BC�ڵ�E������EF��
��1����֤���ı���ABEF�����Σ�
��2������CF������ABC=60�㣬AB= 4��AF =2DF����CF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������ݣ����������������⣺
![]() ����֪����
����֪����![]() ��
��![]() ������
������![]() ��
��
![]() ����
����![]() ��ͬ�ķ����ɼ����
��ͬ�ķ����ɼ����![]() ��
��![]() ��
��
![]() �������ϵ�ѧϰ���̣��ɲ²���ۣ�
�������ϵ�ѧϰ���̣��ɲ²���ۣ�![]() ________��
________��
![]() �������ϵĽ��ۼ������¸��⣺��
�������ϵĽ��ۼ������¸��⣺��![]() ________����
________����![]() =________��
=________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������l1��y=![]() ��x��2��2��2��x��ֱ���O��A���㣬��������l1����ƽ�Ƶõ�l2 �� ����A��AB��x�ύ������l2�ڵ�B�������������l1��l2��ֱ��AB��y����Χ�ɵ���Ӱ���ֵ����Ϊ16����������l2�ĺ�������ʽΪ��������
��x��2��2��2��x��ֱ���O��A���㣬��������l1����ƽ�Ƶõ�l2 �� ����A��AB��x�ύ������l2�ڵ�B�������������l1��l2��ֱ��AB��y����Χ�ɵ���Ӱ���ֵ����Ϊ16����������l2�ĺ�������ʽΪ��������
A.y=![]() ��x��2��2+4
��x��2��2+4
B.y=![]() ��x��2��2+3
��x��2��2+3
C.y=![]() ��x��2��2+2
��x��2��2+2
D.y=![]() ��x��2��2+1
��x��2��2+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ����x��Ľ���ĺ�����ֱ�Ϊ��1��3�������н�����ȷ�ĸ����У�������
��ac��0����2a+b=0����4a+2b+c��0���ܶ�������x����ax2+bx��a+b��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����OABC�����ODEF��λ��ͼ�Σ�P��λ�����ģ�����B������Ϊ��2��4������E������Ϊ����1��2�������P������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=8,AD=5����E![]() ΪDC����һ�����㣬�ѡ�ADE��AE�۵�����D�Ķ�Ӧ��D�����ھ���ABCD�ĶԳ�����ʱ��DE�ij�Ϊ____________.
ΪDC����һ�����㣬�ѡ�ADE��AE�۵�����D�Ķ�Ӧ��D�����ھ���ABCD�ĶԳ�����ʱ��DE�ij�Ϊ____________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ѧ����У�С��Ϊ�˲���У�����AB�ĸ߶ȣ�վ�ڽ�ѧ¥�ϵ�C�������˵Ͷ�B�ĸ���Ϊ45�㣬�����˶���A������Ϊ30�㣬��������ѧ¥��ˮƽ����CDΪ9m������˵ĸ߶��Ƕ��٣�������������ţ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com