Question

【题目】如图，正方形ABCD的边长为8cm，E、F、G、H分别是AB、BC、CD、DA 上的动点，且AE=BF=CG=DH.

（1）求证：四边形EFGH是正方形；

（2）判断直线EG是否经过一个定点，并说明理由；

（3）求四边形EFGH面积的最小值。

Answer 1

【答案】(1)证明见解析；

（2）直线EG经过一个定点，这个定点为正方形的中心（AC、BD的交点）；理由见解析；

（3）32cm2.

【解析】

试题分析：（1）由正方形的性质得出∠A=∠B=∠C=∠D=90°，AB=BC=CD=DA，证出AH=BE=CF=DG，由SAS证明△AEH≌△BFE≌△CGF≌△DHG，得出EH=FE=GF=GH，∠AEH=∠BFE，证出四边形EFGH是菱形，再证出∠HEF=90°，即可得出结论；

（2）连接AC、EG，交点为O；先证明△AOE≌△COG，得出OA=OC，证出O为对角线AC、BD的交点，即O为正方形的中心；

（3）设四边形EFGH面积为S，BE=xcm，则BF=（8-x）cm，由勾股定理得出S=x2+（8-x）2=2（x-4）2+32，S是x的二次函数，容易得出四边形EFGH面积的最小值．

试题解析：【解答】（1）证明：∵四边形ABCD是正方形，

∴∠A=∠B=∠C=∠D=90°，AB=BC=CD=DA，

∵AE=BF=CG=DH，

∴AH=BE=CF=DG，

在△AEH、△BFE、△CGF和△DHG中，

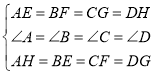
∴△AEH≌△BFE≌△CGF≌△DHG（SAS），

∴EH=FE=GF=GH，∠AEH=∠BFE，

∴四边形EFGH是菱形，

∵∠BEF+∠BFE=90°，

∴∠BEF+∠AEH=90°，

∴∠HEF=90°，

∴四边形EFGH是正方形；

（2）解：直线EG经过一个定点，这个定点为正方形的中心（AC、BD的交点）；理由如下：

连接AC、EG，交点为O；如图所示：

∵四边形ABCD是正方形，

∴AB∥CD，

∴∠OAE=∠OCG，

在△AOE和△COG中，

，

∴△AOE≌△COG（AAS），

∴OA=OC，即O为AC的中点，

∵正方形的对角线互相平分，

∴O为对角线AC、BD的交点，即O为正方形的中心；

（3）解：设四边形EFGH面积为S，设BE=xcm，则BF=（8-x）cm，

根据勾股定理得：EF2=BE2+BF2=x2+（8-x）2，

∴S=x2+（8-x）2=2（x-4）2+32，

∵2＞0，

∴S有最小值，

当x=4时，S的最小值=32，

∴四边形EFGH面积的最小值为32cm2．