
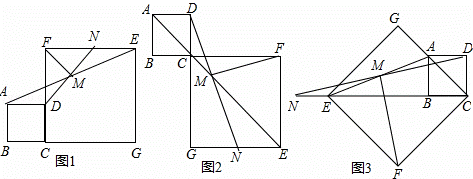
如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥F M(无需写证明过程)
M(无需写证明过程)
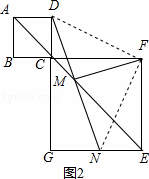
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
解:(1)如图2,DM=FM,DM⊥FM,
证明:连接DF,NF,
∵四边形ABCD和CGEF是正方形,
∴AD∥BC,BC∥GE,
∴AD∥GE,
∴∠DAM=∠NEM,
∵M是AE的中点,
∴AM=EM,
在△MAD与△MEN中,
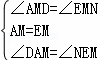 ,
,
∴△MAD≌△MEN,
∴DM=MN,AD=EN,
∵AD=CD,
∴CD=NE,
∵CF=EF,∠DCF=∠DCB=90°,
在△DCF与△NEF中,
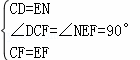 ,
,
∴△MAD≌△MEN,
∴DF=NF,∠CFD=∠EFN,
∵∠EFN+∠NFC=90°,
∴∠DFC+∠CFN=90°,
∴∠DFN=90°,
∴DM⊥FM,DM=FM
(2)猜想:DM⊥FM,DM=FM,
证明如下:如图3,连接DF,NF,
连接DF,NF,
∵四边形ABCD是正方形,
∴AD∥BC,
∵点E、B、C在同一条直线上,
∴AD∥CN,
∴∠ADN=∠MNE,
在△MAD与△MEN中,
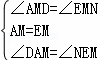 ,
,
∴△MAD≌△MEN,
∴DM=MN,AD=EN,
∵AD=CD,
∴CD=NE,
∵CF=EF,
∵∠DCF=9 0°+45°=135°,∠NEF=180°﹣45°=135°,
0°+45°=135°,∠NEF=180°﹣45°=135°,
∴∠DCF=∠NEF,
在△DCF与△NEF中,
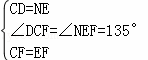 ,
,
∴△MAD≌△MEN,
∴DF=NF,∠CFD=∠EFN,
∵∠CFD+∠EFD=90°,
∴∠NFE+∠EFD=90°,
∴∠DFN=90°,
∴DM⊥FM,DM=FM.



科目:初中数学 来源: 题型:
“魅力凉都六盘水”某周连续7天的最高气温(单位°C)是26,24,23,18,22,22,25,则这组数据的中位数是( )
A.18 B.22  C.23 D.24
C.23 D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
如果抛物线 过定点M(1,1),则称次
过定点M(1,1),则称次 抛物线为定点抛物线。
抛物线为定点抛物线。
(1)张老师在投影屏 幕上出示了一个题目:请你写出一条定点抛物线的一个解析式。小敏写出了一个答案:
幕上出示了一个题目:请你写出一条定点抛物线的一个解析式。小敏写出了一个答案: ,请你写出一个不同于小敏的答案;
,请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线 ,求该抛物线顶点纵坐标的值最小时的解析式,请你解答。
,求该抛物线顶点纵坐标的值最小时的解析式,请你解答。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图10,在△AFD和△CEB中,点A、E、F、C在同一条直线上,有下面四个结断:①AD=CB;②AE=CF;③∠B=∠D;④AD∥BC.请用其中三个作为条件,余下的一个作为结论编一道数学题,并证明结论成立.
 |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com