
 如图,已知:抛物线与坐标轴相交于点A、B、C,顶点D的坐标为D(-1,4),又知C(-4,0)
如图,已知:抛物线与坐标轴相交于点A、B、C,顶点D的坐标为D(-1,4),又知C(-4,0)| 4 |
| 9 |
| 32 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 32 |
| 9 |
| 32 |
| 9 |
| 32 |
| 9 |
| 4 |
| 9 |
|
|
| 4 |
| 3 |
| 8 |
| 3 |

| 8 |
| 3 |
| 8 |
| 3 |
| 32 |
| 9 |
| 8 |
| 3 |
| 8 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 28 |
| 3 |
| 4 |
| 3 |


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
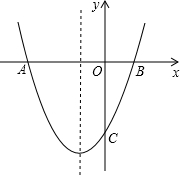 (2011•利川市一模)如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).
(2011•利川市一模)如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).查看答案和解析>>
科目:初中数学 来源:江苏省苏州吴江市2010届初三上学期期末考试数学试题 题型:059
如图,已知:抛物线![]() 与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是
与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是![]() ,连结AC.
,连结AC.

(1)B、C两点坐标分别为B(________,________)、C(________,________),抛物线的函数关系式为________;
(2)判断△ABC的形状,并说明理由;
(3)在△ABC内部能否截出面积最大的矩形DEFC(顶点D、E、F、G在△ABC各边上)?若能,求出在AB边上的矩形顶点的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
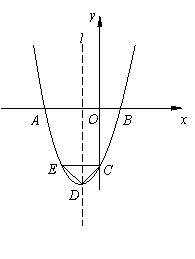
如图,已知:抛物线![]() 与x轴相交于A、B两点,与y轴相交于点C,并且OA = OC.
与x轴相交于A、B两点,与y轴相交于点C,并且OA = OC.
(1)求这条抛物线的解析式;
(2)过点C作CE // x轴,交抛物线于点E,设抛物线的顶点为点D,试判断△CDE的形状,并说明理由;
(3)设点M在抛物线的对称轴l上,且△MCD的面积等于△CDE的面积,请写出点M的坐标(无需写出解题步骤).
查看答案和解析>>
科目:初中数学 来源:2009-2010学年浙江省丽水市云和二中九年级(上)期中数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com