
分析 (1)仿照已知解题方法将原式变形即可;
(2)根据(1)的结果,利用非负数的性质求出最小值即可.
解答 解:(1)设-x4-8x2+10=(-x2+1)(x2+a)+b=-x4-(a-1)x2+(a+b),
∴$\left\{\begin{array}{l}{a-1=8}\\{a+b=10}\end{array}\right.$,
解得:a=9,b=1,
则原式=$\frac{(-{x}^{2}+1)({x}^{2}+9)+1}{-{x}^{2}+1}$=x2+9+$\frac{1}{-{x}^{2}+1}$;
(2)由原式=x2+9+$\frac{1}{-{x}^{2}+1}$,
得到当x=0时,x2+9与$\frac{1}{-{x}^{2}+1}$分别取得最小值,
则x=0时,原式的最小值为10.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:选择题
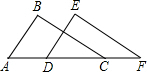 如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )| A. | ∠A=∠EDF | B. | ∠B=∠E | C. | ∠BCA=∠F | D. | BC∥EF |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
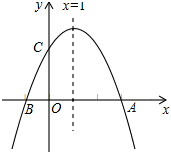 如图:二次函数y=ax2+bx+c的图象与x轴交A、B两点,与y轴交于C点,且对称轴为x=1,点B的坐标是(-1,0),则下面四个结论:①2a+b=0,②4a-2b+c<0,③ac<0,④当y<0时,x<-1或x>3,其中正确的个数是( )
如图:二次函数y=ax2+bx+c的图象与x轴交A、B两点,与y轴交于C点,且对称轴为x=1,点B的坐标是(-1,0),则下面四个结论:①2a+b=0,②4a-2b+c<0,③ac<0,④当y<0时,x<-1或x>3,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )
如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )| A. | $\frac{{3+\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com