
【题目】已知:在△ABC中,AC=a,AB与BC所在直线成45°角,AC与BC所在直线形成的夹角的余弦值为 ![]() (即cosC=
(即cosC= ![]() ),则AC边上的中线长是 .
),则AC边上的中线长是 .
【答案】![]() a或
a或 ![]() a
a
【解析】解:分两种情况: ①如图1.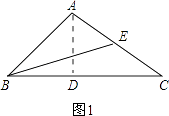
作△ABC的高AD,BE为AC边的中线.
∵在直角△ACD中,AC=a,cosC= ![]() ,
,
∴CD= ![]()
![]() a,AD=
a,AD= ![]() a.
a.
∵在直角△ABD中,∠ABD=45°,
∴BD=AD= ![]() a,
a,
∴BC=BD+CD= ![]() a.
a.
在△BCE中,由余弦定理,得
BE2=BC2+EC2﹣2BCECcosC
= ![]() a2+
a2+ ![]() a2﹣2×
a2﹣2× ![]() a×
a× ![]() a×
a× ![]()
= ![]() a2 ,
a2 ,
∴BE= ![]() a;
a;
②如图2.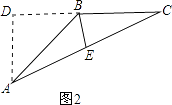
作△ABC的高AD,BE为AC边的中线.
∵在直角△ACD中,AC=a,cosC= ![]() ,
,
∴CD= ![]() a,AD=
a,AD= ![]() a.
a.
∵在直角△ABD中,∠ABD=45°,
∴BD=AD= ![]() a,
a,
∴BC=CD﹣BD= ![]() a.
a.
在△BCE中,由余弦定理,得
BE2=BC2+EC2﹣2BCECcosC
= ![]() a2+
a2+ ![]() a2﹣2×
a2﹣2× ![]() a×
a× ![]() a×
a× ![]()
= ![]() a2 ,
a2 ,
∴BE= ![]() a.
a.
综上可知AC边上的中线长是 ![]() a或
a或 ![]() a.
a.
所以答案是: ![]() a或
a或 ![]() a.
a.
【考点精析】本题主要考查了解直角三角形的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB:BC=3:4,AC=5,点P从点A出发,以每秒1个单位的速度,沿△ABC边A→B→C→A的方向运动,运动时间为t秒.
(1)求AB与BC的长;
(2)在点P的运动过程中,是否存在这样的点P,使△CDP为等腰三角形?若存在,求出t值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′,点B′恰好落在BC边土,B′C′和CD交于点P,则∠B′PD的度数是( )

A. 105° B. 120° C. 130° D. 135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯的高度,测得电梯楼顶部B处的仰角为45°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC(结果精确到0.1米)(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)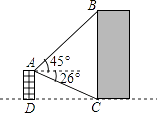
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求代数式的值.
(1)(6a2﹣2ab)﹣2(3a2+4ab﹣![]() b2)其中a=
b2)其中a=![]() ,b=﹣1.
,b=﹣1.
(2)已知A=a2﹣2ab+b2,B=a2+2ab+b2
①求2A﹣B;
②如果2A﹣3B+C=0,那么C的表达式是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年9月,莉莉进入八中初一,在准备开学用品时,她决定购买若干个某款笔记本,甲、乙两家文具店都有足够数量的该款笔记本,这两家文具店该款笔记本标价都是20元/个.甲文具店的销售方案是:购买该笔记本的数量不超过5个时,原价销售;购买该笔记本超过5个时,从第6个开始按标价的八折出售:乙文具店的销售方案是:不管购买多少个该款笔记本,一律按标价的九折出售.
(1)若设莉莉要购买x(x>5)个该款笔记本,请用含x的代数式分别表示莉莉到甲文具店和乙文具店购买全部该款笔记本所需的费用;
(2)在(1)的条件下,莉莉购买多少个笔记本时,到乙文具店购买全部笔记本所需的费用与到甲文具店购买全部笔记本所需的费用相同?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com