
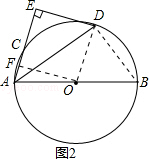
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E. 
(1)求证:DE是⊙O的切线;
(2)如果AD=5,AE=4,求AC长.
【答案】
(1)证明:连接OD,如图1所示:
∵AD为∠CAB的平分线,
∴∠CAD=∠BAD,
又∵OA=OD,
∴∠BAD=ODA,
∴∠CAD=∠ODA,
∴AC∥OD,
∴∠E+∠EDO=180°,
又∵AE⊥ED,即∠E=90°,
∴∠EDO=90°,
则ED为圆O的切线

(2)解:连接BD,如图2所示,过点A作AF⊥AC,
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△ABD中,cos∠DAB= ![]() ,
,
在Rt△AED中,AE=4,AD=5,
∴cos∠EAD= ![]() =
= ![]() ,又∠EAD=∠DAB,
,又∠EAD=∠DAB,
∴cos∠DAB=cos∠EAD= ![]() =
= ![]() ,
,
则AB= ![]() AD=
AD= ![]() ,即圆的直径为
,即圆的直径为 ![]() ,
,
∴AO= ![]() ,
,
∵∠E=∠EDO=∠EFO=90°,
∴四边形EFOD是矩形,
∴OF=DE=3,
∴AF= ![]() =
= ![]() ,
,
∴AC=2AF= ![]() .
.
【解析】(1)连接OD,由AD为角平分线,得到一对角相等,再由OA=OD,得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行可得AE与OD平行,由两直线平行同旁内角互补,得到∠E与∠EDO互补,再由∠E为直角,可得∠EDO为直角,即DE为圆O的切线,得证;(2)连接BD,过点A作AF⊥AC,由AB为圆O的直径,根据直径所对的圆周角为直角,得到∠ADB为直角,在直角三角形ABD中,利用锐角三角函数定义得到cos∠DAB的值,又在直角三角形AED中,由AE及AD的长,利用锐角三角函数定义求出cos∠EAD的值,由∠EAD=∠DAB,得到cos∠EAD=cos∠DAB,得出cos∠DAB的值,即可求出直径AB的长,由勾股定理和垂径定理即可求出AC长.


科目:初中数学 来源: 题型:
【题目】如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
例如:方程![]() 的解为
的解为![]() ,不等式组
,不等式组![]() 的解集为
的解集为![]() ,因为
,因为![]() ,所以,称方程
,所以,称方程![]() 为不等式组
为不等式组![]() 的关联方程.
的关联方程.
(1)在方程①![]() ,②
,②![]() ,③
,③![]() 中,不等式组
中,不等式组![]() 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)
(2)若不等式组 的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
(3)若方程![]() ,
,![]() 都是关于
都是关于![]() 的不等式组
的不等式组![]() 的关联方程,求
的关联方程,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( )度. 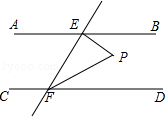
A.70
B.65
C.60
D.55
查看答案和解析>>
科目:初中数学 来源: 题型:
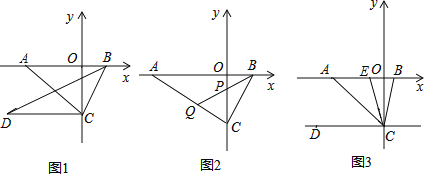
【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,![]() ,
,![]() ,其中a、b满足关系式:
,其中a、b满足关系式:![]() .
.
![]() ______,
______,![]() ______,
______,![]() 的面积为______;
的面积为______;
![]() 如图2,石
如图2,石![]() 于点C,点P是线段OC上一点,连接BP,延长BP交AC于点
于点C,点P是线段OC上一点,连接BP,延长BP交AC于点![]() 当
当![]() 时,求证:BP平分
时,求证:BP平分![]() ;
;![]() 提示:三角形三个内角和等于
提示:三角形三个内角和等于![]()
![]() 如图3,若
如图3,若![]() ,点E是点A与点B之间上一点连接CE,且CB平分
,点E是点A与点B之间上一点连接CE,且CB平分![]() 问
问![]() 与
与![]() 有什么数量关系?请写出它们之间的数量关系并请说明理由.
有什么数量关系?请写出它们之间的数量关系并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB.
(1)用没有刻度的直尺和圆规按所给的要求作图:点C在线段BA的延长线上,且CA=AB;
(2)在(1)中,如果AB=28 cm,线段BC上有一点M,且线段AM∶BM=1∶3,求线段CM的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).


图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个圆柱的底面半径是10 cm,高是18 cm,把这个圆柱放在水平桌面上,如图所示.
(1)如果用一个平面沿水平方向去截这个圆柱,所得的截面是什么形状?
(2)如果用一个平面沿竖直方向去截这个圆柱,所得的截面是什么形状?
(3)怎样截时所得的截面是长方形且长方形的面积最大,请你画出这个截面并求其面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿射线AC的方向匀速平移得到△PNM,速度为1cm/s,同时,点Q从点C出发,沿射线CB方向匀速运动,速度为1cm/s,当△PNM停止平移时,点Q也停止运动,如图2所示,设运动时间为t(s)(0<t<4).
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使得PQ=QM,若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=150°,点A到BC的距离为1,与AB重合的一条射线AP,从AB开始,以每秒15°的速度绕点A逆时针匀速旋转,到达AC后立即以相同的速度返回AB,到达后立即重复上述旋转过程,设AP与BC边的交点为M,旋转2019秒时,BM= , CM= . 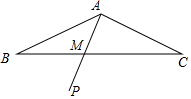
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com