
【题目】如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6 . 其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( ) 
A.86
B.64
C.54
D.48
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】某校学生来自甲、乙、丙三个地区,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自甲地区的为180人,则下列说法不正确的是【 】

A.扇形甲的圆心角是72°
B.学生的总人数是900人
C.丙地区的人数比乙地区的人数多180人
D.甲地区的人数比丙地区的人数少180人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.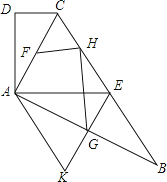
(1)求证:AC2=CDBC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB.
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是平行四边形;
(2)若AB=6,AC=10,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com