
【题目】已知抛物线y=x2+bx﹣3(b是常数)经过点A(﹣1,0).
(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P'.
①当点P'落在该抛物线上时,求m的值;
②当点P'落在第二象限内,P'A2取得最小值时,求m的值.
【答案】
(1)
解:∵抛物线y=x2+bx﹣3经过点A(﹣1,0),
∴0=1﹣b﹣3,解得b=﹣2,
∴抛物线解析式为y=x2﹣2x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线顶点坐标为(1,﹣4);
(2)
解:①由P(m,t)在抛物线上可得t=m2﹣2m﹣3,
∵点P′与P关于原点对称,
∴P′(﹣m,﹣t),
∵点P′落在抛物线上,
∴﹣t=(﹣m)2﹣2(﹣m)﹣3,即t=﹣m2﹣2m+3,
∴m2﹣2m﹣3=﹣m2﹣2m+3,解得m= ![]() 或m=﹣
或m=﹣ ![]() ;
;
②由题意可知P′(﹣m,﹣t)在第二象限,
∴﹣m<0,﹣t>0,即m>0,t<0,
∵抛物线的顶点坐标为(1,﹣4),
∴﹣4≤t<0,
∵P在抛物线上,
∴t=m2﹣2m﹣3,
∴m2﹣2m=t+3,
∵A(﹣1,0),P′(﹣m,﹣t),
∴P′A2=(﹣m+1)2+(﹣t)2=m2﹣2m+1+t2=t2+t+4=(t+ ![]() )2+
)2+ ![]() ;
;
∴当t=﹣ ![]() 时,P′A2有最小值,
时,P′A2有最小值,
∴﹣ ![]() =m2﹣2m﹣3,解得m=
=m2﹣2m﹣3,解得m= ![]() 或m=
或m= ![]() ,
,
∵m>0,
∴m= ![]() 不合题意,舍去,
不合题意,舍去,
∴m的值为 ![]() .
.
【解析】(1)把A点坐标代入抛物线解析式可求得b的值,则可求得抛物线解析式,进一步可求得其顶点坐标;(2)①由对称可表示出P′点的坐标,再由P和P′都在抛物线上,可得到关于m的方程,可求得m的值;②由点P′在第二象限,可求得t的取值范围,利用两点间距离公式可用t表示出P′A2 , 再由点P′在抛物线上,可用消去m,整理可得到关于t的二次函数,利用二次函数的性质可求得其取得最小值时t的值,则可求得m的值.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,下列正方形网格的每个小正方形的边长均为1,⊙O的半径为n≥8 ![]() .规定:顶点既在圆上又是正方形格点的直角三角形称为“圆格三角形”,请按下列要求各画一个“圆格三角形”,并用阴影表示出来.
.规定:顶点既在圆上又是正方形格点的直角三角形称为“圆格三角形”,请按下列要求各画一个“圆格三角形”,并用阴影表示出来.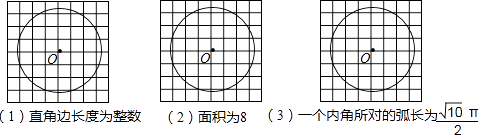
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x-1与反比例函数y= ![]() 的图像交于点A(2,1),B(-1,-2),则使y1>y2的x的取值范围是( ).
的图像交于点A(2,1),B(-1,-2),则使y1>y2的x的取值范围是( ).
A.x>2
B.x>2或-1<x<0
C.-1<x<2
D.x>2或x<-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“兰州中山桥“位于兰州滨河路中段白塔山下、金城关前,是黄河上第一座真正意义上的桥梁,有“天下黄河第一桥“之美誉.它像一部史诗,记载着兰州古往今来历史的变迁.桥上飞架了5座等高的弧形钢架拱桥. 小芸和小刚分别在桥面上的A,B两处,准备测量其中一座弧形钢架拱梁顶部C处到桥面的距离AB=20m,小芸在A处测得∠CAB=36°,小刚在B处测得∠CBA=43°,求弧形钢架拱梁顶部C处到桥面的距离.(结果精确到0.1m)(参考数据sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(1)本次接受调查的跳水运动员人数为 , 图①中m的值为;
(2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM= ![]() AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是
AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是 ![]() ,则
,则 ![]() 的值是 .
的值是 . 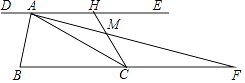
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动,在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°,再过点N作AC的垂线交AB于点F,连接MF,将△MNF关于直线NF对称后得到△ENF,已知AC=8cm,BC=4cm,设点M运动时间为t(s),△ENF与△ANF重叠部分的面积为y(cm2).
(1)在点M的运动过程中,能否使得四边形MNEF为正方形?如果能,求出相应的t值;如果不能,说明理由;
(2)求y关于t的函数解析式及相应t的取值范围;
(3)当y取最大值时,求sin∠NEF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)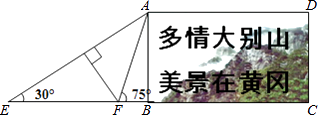
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B、C是直径为6cm的⊙O上的点,且AB=3cm,AC=3 ![]() cm,则∠BAC的度数为( )
cm,则∠BAC的度数为( )
A.15°
B.75°或15°
C.105°或15°
D.75°或105°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com