练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．二元一次方程组$\left\{\begin{array}{l}{x-2y=-3}\\{3x+y=5}\end{array}\right.$的解满足2x-ky=1，求k的值．

    分析 求出方程组的解，代入已知方程计算即可求出k的值．

    解答 解：$\left\{\begin{array}{l}{x-2y=-3①}\\{3x+y=5②}\end{array}\right.$，
    ①+②×2得：7x=7，即x=1，
    把x=1代入①得：y=2，
    ∴方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$，
    代入2x-ky=1中得：2-2k=1，
    解得：k=$\frac{1}{2}$．

    点评 此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．如果规定a*b=$\frac{ab}{a+b}$，比较2*3=$\frac{2×3}{2+3}$=$\frac{5}{6}$．
    （1）写出○*△的表达式（用○和△表示）
    ○*△=$\frac{o×△}{o+△}$；
    （2）求2*（-3）的值；
    （3）求|3*（-4）|的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

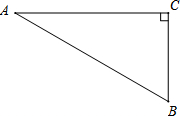    2．已知：如图，在△ABC中，∠C=90°，∠A=30°．
    （1）用直尺和圆规作AB的垂直平分线，分别交AC、AB于点E、D（保留作图痕迹，不写作法）．
    （2）猜想AC与CE之间的数量关系，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知关于x的一元二次方程x2+mx+m-1=0有两个相等的实数根．求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知：如图，∠1=∠2，∠C=∠D，求证：△OAC≌△OBD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

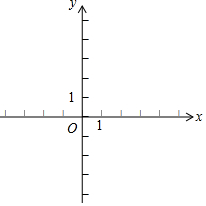    16．在平面直角坐标系中，如果某点P的横坐标和纵坐标相等，则称点P为“梦之点”．例如点（1，1），（-2016，-2016），（-$\sqrt{3}$，-$\sqrt{3}$），…，都是“梦之点”．
    （1）分别判断函数y=-2x+1和y=x2+1的图象上是否存在“梦之点”？若存在，求出点“梦之点”的坐标；
    （2）若二次函数y=ax2+4x+c的图象上有且只有一个“梦之点”（$\frac{3}{2}$，$\frac{3}{2}$），且当0≤x≤m时，函数y=ax2+4x+c-$\frac{3}{4}$（a≠0）的最小值为-3，最大值为1，求m的取值范围；
    （3）直线l：y=kx+2经过“梦之点”P，与x轴交于点D，与反比例函数y=$\frac{n}{x}$的图象交于M，N两点（点M在点N的左侧），若点P的横坐标为1，且满足DM+DN＜3$\sqrt{2}$，请直接写出n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

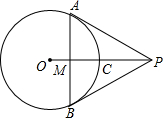    3．如图，PA，PB与⊙O相切于点A，B，连接AB，PO交⊙O于点C，交AB于点M．
    （1）求证：点C是△APB的内心；
    （2）若AB=MP=4，求PC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

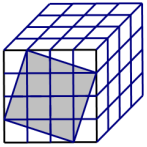    20．魔方，又叫魔术方块，也称鲁比克方块，是匈牙利布达佩斯建筑学院厄尔诺•鲁比克教授在1974年发明的．魔方与中国人发明的“华容道”，法国人发明的“独立钻石”一同被称为智力游戏界的三大不可思议．如图是一个4阶魔方，又称“魔方的复仇”，由四层完全相同的64个小立方体组成，体积为64cm3．
    （1）求组成这个魔方的小立方体的棱长．
    （2）图中阴影部分是一个正方形，则该阴影部分正方形的面积为10 cm2．边长是$\sqrt{10}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

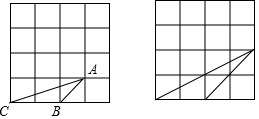    1．在方格纸中，每个格子的顶点叫做格点，以格点连线为边的三角形叫做格点三角形，如图所示，在大小为4×4的正方形方格中，存在格点△ABC，请根据三边的比对应相等的三角形是相似三角形的原理，在图中画一个与△ABC相似但不全等的格点△A1B1C1，并说明理由．

    查看答案和解析>>

    同步练习册答案