
分析 (1)根据题意列式计算即可;
(2)设至少抽掉了x张黑桃,放入x张的红桃,根据题意列不等式即可得到结论;
(3)根据题意即可得到结论.
解答 解:(1)抽出一张是红桃的概率是$\frac{9}{9+10+11}$=$\frac{3}{10}$;
(2)设至少抽掉了x张黑桃,放入x张的红桃,
根据题意得,$\frac{9+x}{9+10+11}$≥$\frac{2}{5}$,
解得:x≥3,
答:至少抽掉了3张黑桃;
(3)当m为10时,事件“再抽出的这张牌是方块”为必然事件,
当m为9,8,7时,事件“再抽出的这张牌是方块”为随机事件事件,
P(最小)=$\frac{11}{(10-7)+11}$=$\frac{11}{14}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.同时考查了必然事件、不可能事件与随机事件的定义.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{9}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
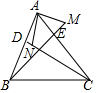 如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是90°.
如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com