
【题目】给出下列判断:
①一组对边平行,另一组对边相等的四边形是平行四边形.
②对角线相等的四边形是矩形.
③对角形互相垂直且相等的四边形是正方形.
④有一条对角线平分一个内角的平行四边形为菱形.
其中,不正确的有( )
A.1个
B.2个
C.3个
D.4个
科目:初中数学 来源: 题型:
【题目】某地一周内每天的最高气温与最低气温记录如下表:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
最高气温 | 10℃ | 12℃ | 11℃ | 9℃ | 7℃ | 5℃ | 7℃ |
最低气温 | 2℃ | 1℃ | 0℃ | ﹣1℃ | ﹣4℃ | ﹣5℃ | ﹣5℃ |
则温差最大的一天是星期_____;这一天温差为_____℃.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
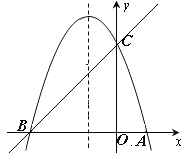
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.
⑴若直线y=mx+n经过B,C两点,求直线BC和抛物线的解析式;
⑵在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求点M的坐标;⑶设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
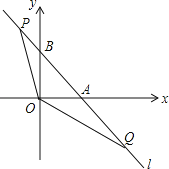
【题目】如图,直线l:y=﹣x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.
(1)求△AOB的周长;
(2)设AQ=t>0,试用含t的代数式表示点P的坐标;
(3)当动点P,Q在直线l上运动到使得△AOQ与△BPO的周长相等时,记tan∠AOQ=m,若过点A的二次函数y=ax2+bx+c同时满足以下两个条件:
①6a+3b+2c=0;
②当m≤x≤m+2时,函数y的最大值等于![]() ,求二次项系数a的值.
,求二次项系数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
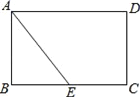
【题目】如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是______ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
小军同学在学校组织的社会实践活动中,负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表:
月 均 用水量 |
|
|
|
|
|
|
|
频数 | 2 | 12 | ① | 10 | ② | 3 | 2 |
百分比 | 4% | 24% | 30% | 20% | ③ | 6% | 4% |
⑴请根据题中已有的信息补全频数分布表:① ,② ,③ ;
⑵如果家庭月均用水量“大于或等于5
⑶记月均用水量在![]() 范围内的两户为
范围内的两户为![]() 、
、![]() ,在
,在![]() 范围内3户为
范围内3户为![]() 、
、![]() 、
、![]() ,从这5户家庭中任意抽取2户,试完成下表,并求出抽取的2户家庭来自不同范围的概率.
,从这5户家庭中任意抽取2户,试完成下表,并求出抽取的2户家庭来自不同范围的概率.
|
|
|
|
| |
| |||||
| |||||
| |||||
| |||||
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com