
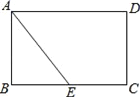
【题目】如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是______ cm.
【答案】![]()
【解析】如图所示:过点B′作B′F⊥BC,垂足为F,连接B′C.首先求得AE=5.然后在求得OE=![]() .,OB=
.,OB=![]() ,由翻折的性质可知BB′=
,由翻折的性质可知BB′=![]() ,接下来证明△BOE∽△BFB′,由相似三角形的性质可得到:
,接下来证明△BOE∽△BFB′,由相似三角形的性质可得到:![]() ,
,![]() ,从而可求得FC=
,从而可求得FC=![]() ,Rt△B′FC中,由勾股定理可求得B′C=
,Rt△B′FC中,由勾股定理可求得B′C=![]() .
.
解:如图所示:过点B′作B′F⊥BC,垂足为F,连接B′C.
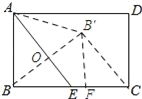
∵点E是BC的中点,
∴BE=![]() .
.
在Rt△ABE中,AE=![]() .
.
由射影定理可知;OEAE=BE2,
∴OE=![]() .
.
由翻折的性质可知;BO⊥AE.
∴![]() .
.
∴OB=![]() .
.
∴BB′=![]() .
.
∵∠OBE=∠FBB′,∠BOE=∠BFB′,
∴△BOE∽△BFB′.
∴![]() =
=![]() ,即
,即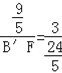 =
=![]() .
.
解得:![]() ,
,![]() .
.
∴FC=![]() .
.
在Rt△B′FC中,B′C=![]() =
=![]() .
.
故答案为:![]() .
.
“点睛”本题主要考查的是翻折的性质、勾股定理、相似三角形的性质和判定,求得B′F、BF的长度是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
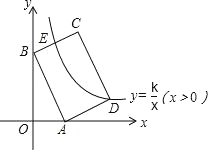
【题目】如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=![]() (x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为 .
(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
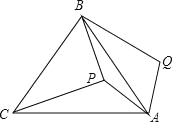
【题目】如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
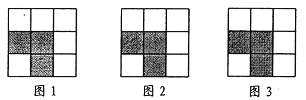
【题目】下列3×3网格都是由9个相同小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形。
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列判断:
①一组对边平行,另一组对边相等的四边形是平行四边形.
②对角线相等的四边形是矩形.
③对角形互相垂直且相等的四边形是正方形.
④有一条对角线平分一个内角的平行四边形为菱形.
其中,不正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知△OAB、△OBC、△OCD、△ODE、△OEF和△OFA均为边长为a的等边三角形,点P为边BC上任意一点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)那么∠MPN=______,并求证PM+PN=3a;
(2)如图2,联结OM、ON.求证:OM=ON;
(3)如图3,OG平分∠MON,判断四边形OMGN是否为特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
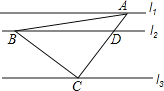
【题目】如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾已经成为时下最普遍与敏感的话题.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了尚不完整的统计图表.
级别 | 观 点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |

请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中E组所占的百分比为 %;
(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com