
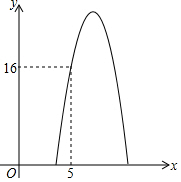
 某商品的进价为每个3元,已知该商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=ax2+16x+c,其图象如图所示.
某商品的进价为每个3元,已知该商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=ax2+16x+c,其图象如图所示.分析 (1)利用待定系数法求二次函数解析式得出即可;
(2)利用配方法求出二次函数最值即可;
(3)根据题意令y=16,解方程可得x的值,结合图象可知x的范围.
解答 解:(1)y=ax2+16x+c图象过点(3,0)、(5,16),
∴$\left\{\begin{array}{l}{9a+48+c=0}\\{25a+80+c=16}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{c=-39}\end{array}\right.$.
(2)∵y=-x2+16x-39=-(x-8)2+25,
∴当x=8时,y最大=25.
答:销售单价为8元时,该种商品每天的销售利润最大,最大利润为25元;
(3)根据题意,当y=16时,得:-x2+16x-39=16,
解得:x1=5,x2=11,
即销售单价5≤x≤11时,该种商品每天的销售利润不低于16元.
点评 本题考查了二次函数的应用以及待定系数法求二次函数解析式等知识,正确利用二次函数图象是解题关键.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:选择题
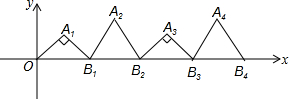 如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )| A. | (4029,1) | B. | (2015,$\sqrt{3}$) | C. | (4030,1) | D. | (4029,$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
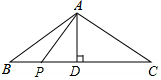 如图,等腰△ABC的底边BC=8cm,腰AC=5cm,AD是底边BC上的高,一动点P在底边上从点B开始向点C以0.25cm/s的速度移动,设运动时间为t(s).
如图,等腰△ABC的底边BC=8cm,腰AC=5cm,AD是底边BC上的高,一动点P在底边上从点B开始向点C以0.25cm/s的速度移动,设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com