
【题目】八(1)班五位同学参加学校举办的数学竞赛,试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分。赛后A,B, C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表:
参赛同学 | 答对题数 | 答错题数 | 未答题数 |
A | 19 | 0 | 1 |
B | 17 | 2 | 1 |
C | 15 | 2 | 3 |
D | 17 | 1 | 2 |
E | / | / | 7 |
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知:A,B,C,D,E五位同学成绩分别是95分,81分,64分,83分,58分.
①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况.请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).
【答案】(1)82.5;(2)①E同学答对12题,答错1题;②C同学,他实际答对14题,答错3题,未答3题.
【解析】
试题(1)直接算出A,B,C,D四位同学成绩的总成绩,再进一步求得平均数即可;
(2)①设E同学答对x题,答错y题,根据对错共20﹣7=13和总共得分58列出方程组成方程组即可;
②根据表格分别算出每一个人的总成绩,与实际成绩对比:A为19×5=95分正确,B为17×5+2×(﹣2)=81分正确,C为15×5+2×(﹣2)=71错误,D为17×5+1×(﹣2)=83正确,E正确;所以错误的是E,多算7分,也就是答对的少一题,打错的多一题,由此得出答案即可.
试题解析:解:(1)![]() (分),
(分),
答:A,B,C,D四位同学成绩的平均分是82.5分.
(2)①设E同学答对x题,答错y题,由题意得
![]() ,解得
,解得![]() .
.
答:E同学答对12题,答错1题.
②C同学,他实际答对14题,答错3题,未答3题.


 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】金堂骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,某车行经营的A型车去年2月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年2月份与去年2月份卖出的A型车数量相同,则今年2月份A型车销售总额将比去年2月份销售总额增加25%.
(1)求今年2月份A型车每辆销售价多少元?
(2)该车行计划今年3月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的2倍,A、B两种型号车的进货和销售价格如下表,问应如何进货才能使这批车获利最多?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图一,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=x-2经过A、C两点,且AB=2.
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设s=![]() ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.
(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两人加工同一种零件,每小时甲比乙多加工10个这种零件,甲加工150个这种零件所用的时间与乙加工120个这种零件所用的时间相等,
(1)甲、乙两人每小时各加工多少个这种零件?
(2)该工厂计划加工920个零件,甲参与加工这批零件不超过12天,则乙至少加工多少天才能加工完这批零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜种植基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.
(1)改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元?
(2)已知改造1个甲种型号大棚的时间是5天,改造1个乙种型号大概的时间是3天,该基地计划改造甲、乙两种蔬菜大棚共8个,改造资金最多能投入128万元,要求改造时间不超过35天,请问有几种改造方案?哪种方案基地投入资金最少,最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
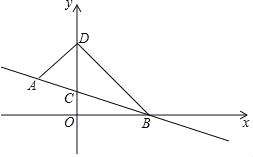
【题目】如图,在平面直角坐标系中,直线AB过点A(﹣1,1),B(2,0),交y轴于点C,点D (0,n)在点C上方.连接AD,BD.
(1)求直线AB的关系式;
(2)求△ABD的面积;(用含n的代数式表示)
(3)当S△ABD=2时,作等腰直角三角形DBP,使DB=DP,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,若直线DF垂直平分AB,垂足为点E,连接BF,CE,且BC=2,下面四个结论:①BF=![]() ;②∠CBF=45°;③△BEC的面积=△FBC的面积;④△ECD的面积为
;②∠CBF=45°;③△BEC的面积=△FBC的面积;④△ECD的面积为![]() ,其中正确的结论有( )
,其中正确的结论有( )
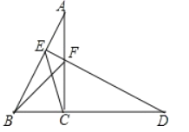
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:
(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶10分钟后,甲、乙两人相距多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com