天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
问题情境：
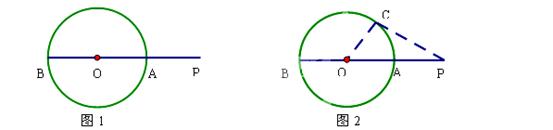
如图1，P是⊙O外的一点，直线PO分别交⊙O于点A、B，则PA是点P到⊙O上的点的最短距离.
探究：
请您结合图2给予证明，
归纳：
圆外一点到圆上各点的最短距离是：这点到连接这点与圆心连线与圆交点之间的距离.
图中有圆，直接运用：
如图3，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于D，P是
上的一个动点，连接AP，则AP的最小值是 ．
|
图中无圆，构造运用：
如图4，在边长为2的菱形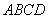
中，∠
=60°，
是
边的中点，
是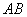
边上一动点，将△
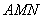沿
所在的直线翻折得到△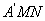
，连接
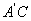,请求出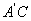长度的最小
值.
 | |||
|
解：由折叠知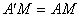
，又M是AD的中点，可得
，故点
在以AD为直径的圆上.如图8，以点M为圆心，MA为半径画⊙M，过M作MH⊥CD，垂足为H，（请继续完成下列解题过程）
迁移拓展，深化运用：
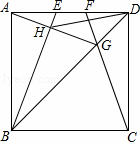
如图6，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是 ．
|
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，直线l∥m，将含有45°角的三角形板ABC的直角顶点C放在直线m
上，若∠1＝25°，则∠2的度数为 【 】
A．20° B．25° C．30° D．35°
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
如图是两个全等的含30°角的直角三角形．
（1）将其相等边拼在一起，组成一个没有重叠部分的平面图形，请你画出所有不同的拼接平面图形的示意图；
（2）若将（1）中平面图形分别印制在质地、形状、大小完全相同的卡片上，洗匀后从中随机抽取一张，求抽取的卡片上平面图形为轴对称图形的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形，边长都为1，则扇形和圆形纸板的面积比是--------（ ）
|
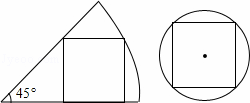
| A． | 5：4 | B． | 5：2 | C． |
| D． |
|
查看答案和解析>>
科目：初中数学 来源： 题型：
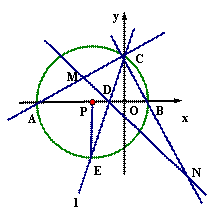
在平面直角坐标系中△ABC的边AB在x轴上，且OA>OB,以AB为直径的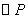
过点C，若C的坐标为（0，2），AB=5, 经过A、B、C三点的抛物线为y=ax2+bx+c。
（1）求点A、B的坐标及抛物线的解析式。
（2）若∠ACB的平分线所在的直线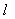
交x轴于点D，交圆于点E。
①求证：PE⊥x轴；
②试求直线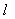对应的一次函数的解析式.
（3）过点D任作一直线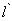
分别交射线CA，CB（点C除外）于点M，N，则
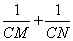的值是否为定值，若是，求出定值，若不是，请说明理由
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，PF⊥DC，求证：⑴AP=EF；⑵AP⊥EF.
：2