
 如图,图象l1反映了某公司产品的销售收入y(单位:元)与销售量x(单位:吨)之间的关系,图象l2反映了该公司产品的产品成本y(元)与销售量x(吨)之间的关系,请根据图中所提供的信息解答下列问题:
如图,图象l1反映了某公司产品的销售收入y(单位:元)与销售量x(单位:吨)之间的关系,图象l2反映了该公司产品的产品成本y(元)与销售量x(吨)之间的关系,请根据图中所提供的信息解答下列问题:
|
|


科目:初中数学 来源: 题型:
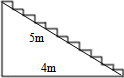 某宾馆准备在大厅的主楼道上铺设某种红色地毯,已知这种地毯售价为30元/m2,主楼道宽2m,其侧面如图,则购买地毯至少需要( )
某宾馆准备在大厅的主楼道上铺设某种红色地毯,已知这种地毯售价为30元/m2,主楼道宽2m,其侧面如图,则购买地毯至少需要( )| A、240元 | B、360元 |
| C、420元 | D、480元 |
查看答案和解析>>
科目:初中数学 来源: 题型:

| A、仅甲正确 |
| B、仅乙正确 |
| C、甲、乙均正确 |
| D、甲、乙均错误 |
查看答案和解析>>
科目:初中数学 来源: 题型:
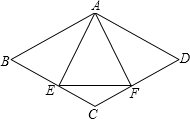 (1)已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且CE=CF.求证:AE=AF.
(1)已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且CE=CF.求证:AE=AF.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
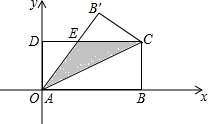 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在B′处.
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在B′处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com