
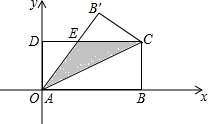
 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在B′处.
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在B′处.| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |


科目:初中数学 来源: 题型:
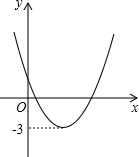 二次函数y=ax2+bx+c(a≠0)的图象如图,若ax2+bx+c=k有两个不相等的实数根,则k的取值范围是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,若ax2+bx+c=k有两个不相等的实数根,则k的取值范围是( )| A、k>-3 | B、k<-3 |
| C、k=-3 | D、无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,图象l1反映了某公司产品的销售收入y(单位:元)与销售量x(单位:吨)之间的关系,图象l2反映了该公司产品的产品成本y(元)与销售量x(吨)之间的关系,请根据图中所提供的信息解答下列问题:
如图,图象l1反映了某公司产品的销售收入y(单位:元)与销售量x(单位:吨)之间的关系,图象l2反映了该公司产品的产品成本y(元)与销售量x(吨)之间的关系,请根据图中所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知:ABCD是正方形,E是AD的中点.
如图,已知:ABCD是正方形,E是AD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
 定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算.比如:
定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算.比如:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com