
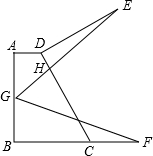
 如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠DCB=60°,AD=2$\sqrt{3}$,BC=6$\sqrt{3}$,点G是线段AB中点,点F在线段BC上,连接GF,将线段GF绕点G逆时针旋转60°,得到线段GE,GE交CD于点H,连结DE,且DE⊥DC,则HE的长为$\frac{8\sqrt{21}}{3}$.
如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠DCB=60°,AD=2$\sqrt{3}$,BC=6$\sqrt{3}$,点G是线段AB中点,点F在线段BC上,连接GF,将线段GF绕点G逆时针旋转60°,得到线段GE,GE交CD于点H,连结DE,且DE⊥DC,则HE的长为$\frac{8\sqrt{21}}{3}$. 分析 过点D作DM⊥BC于点M,过点F作FN⊥GC于N,连接DG、CG,通过解直角三角形求得∠AGD=30°,∠CGB=60°,∠CGD=90°,进而求得∠EDG=150°=∠FCG,∠CGF=∠E,证得△DEG≌△CGF,得出DE=CG=2BG=12,CF=DG=4$\sqrt{3}$,即可求得CN=6,BF=10$\sqrt{3}$,GN=CG+CN=18,根据勾股定理求得FG=4$\sqrt{21}$,然后通过证得△DEH∽△NGF,得出$\frac{HE}{FG}$=$\frac{ED}{GN}$,即可求得HE的长.
解答 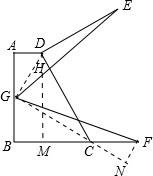 解:过点D作DM⊥BC于点M,过点F作FN⊥GC于N,连接DG、CG,
解:过点D作DM⊥BC于点M,过点F作FN⊥GC于N,连接DG、CG,
∴CM=BC-BM=BC-AD=4$\sqrt{3}$,
∵∠DCB=60°,
∴DM=$\sqrt{3}$CM=12,
∴AG=BG=6,
∵AD=2$\sqrt{3}$,BC=6$\sqrt{3}$,
∴tan∠AGD=$\frac{AD}{AG}$=$\frac{\sqrt{3}}{3}$,tan∠CGB=$\frac{BC}{BG}$=$\sqrt{3}$,
∴∠AGD=30°,∠CGB=60°,
∴∠CGD=90°,∠CDG=60°,∠BCG=30°,
∴∠DGE+∠CGF=90°-∠EGF=30°,
∵∠EDG=∠CDG+∠EDH=150°=180°-∠BCG=∠FCG,
∴∠DGE+∠E=30°,
∴∠CGF=∠E,
在△DEG和△CGF中
$\left\{\begin{array}{l}{∠EDG=∠FCG}\\{∠E=∠CGF}\\{GE=GF}\end{array}\right.$
∴△DEG≌△CGF(AAS),
∴DE=CG=2BG=12,CF=DG=4$\sqrt{3}$,
∴CN=CF•cos∠FCN=6,BF=BC+CF=10$\sqrt{3}$,
∴GN=CG+CN=18,
又FG=$\sqrt{B{G}^{2}+B{F}^{2}}$=$\sqrt{{6}^{2}+(10\sqrt{3})^{2}}$=4$\sqrt{21}$,
∵∠CGF=∠E,∠DHE=∠FNG=90°
∴△DEH∽△NGF,
∴$\frac{HE}{FG}$=$\frac{ED}{GN}$,即$\frac{HE}{4\sqrt{21}}$=$\frac{12}{18}$,
∴HE=$\frac{8\sqrt{21}}{3}$.
故答案为$\frac{8\sqrt{21}}{3}$.
点评 本题考查了旋转的性质,解直角三角函数,三角形全等的判定和性质,三角形相似的判定和性质,勾股定理的应用等,作出辅助线构建全等三角形是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
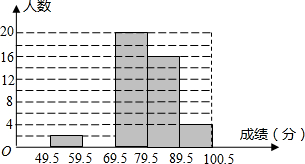 某校初一数学兴趣小组成员小华对本班上期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图:
某校初一数学兴趣小组成员小华对本班上期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图:| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | b |
| 占调查总人数的百分比 | 4% | 16% | m | 32% | n | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com