
【题目】如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3|+(b+3a)2=0. ![]()
(1)求点C表示的数;
(2)点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动,若AP+BQ=2PQ,求时间t;
(3)若点P从A向右运动,点M为AP中点,在P点到达点B之前:① ![]() 的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.
的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.
【答案】
(1)解:∵|a+3|+(b+3a)2=0,
∴a+3=0,b+3a=0,解得a=﹣3,b=9,
∴ ![]() =3,
=3,
∴点C表示的数是3
(2)解:∵AB=9+3=12,点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动,
∴AP=3t,BQ=2t,PQ=12﹣5t.
∵AP+BQ=2PQ,
∴3t+2t=24﹣10t,解得t= ![]() ;
;
还有一种情况,当P运动到Q的左边时,PQ=5t﹣12,方程变为2t+3t=2(5t﹣12),求得t=24/5
(3)解:∵PA+PB=AB为定值,PC先变小后变大,
∴ ![]() 的值是变化的,
的值是变化的,
∴①错误,②正确;
∵BM=PB+ ![]() ,
,
∴2BM=2PB+AP,
∴2BM﹣BP=PB+AP=AB=12
【解析】(1)先根据非负数的性质求出a,b的值,再根据中点的定义得出点C表示的数即可;(2)先用t表示出AP,BQ及PQ的值,再根据AP+BQ=2PQ列出关于t的方程,求出t的值即可;(3)先根据PA+PB=AB,BM=PB+ ![]() 即可得出结论.
即可得出结论.
【考点精析】解答此题的关键在于理解数轴的相关知识,掌握数轴是规定了原点、正方向、单位长度的一条直线.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且a=﹣![]() .
.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是3个,请直接写出a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
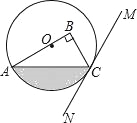
【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com