
分析 分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得BD,CD,再由图形求出BC,在锐角三角形中,BC=BD+CD,在钝角三角形中,BC=CD-BD.
解答 解:(1)如图,锐角△ABC中,AB=4.5,AC=3.9,BC边上高AD=3.6,
在Rt△ABD中,AB=4.5,AD=3.6,由勾股定理得:
BD2=AB2-AD2=4.52-3.62=7.29,
∴BD=2.7,
在Rt△ACD中AC=3.9,AD=3.6,由勾股定理得
CD2=AC2-AD2=3.92-3.62=2.25,
∴CD=1.5,
∴BC的长为BD+DC=2.7+1.5=4.2;
(2)锐角△ABC中,AB=4.5,AC=3.9,BC边上高AD=3.6,
在Rt△ABD中,AB=4.5,AD=3.6,由勾股定理得:
BD2=AB2-AD2=4.52-3.62=7.29,
∴BD=2.7,
在Rt△ACD中AC=3.9,AD=3.6,由勾股定理得
CD2=AC2-AD2=3.92-3.62=2.25,
∴CD=1.5,
∴BC的长为BD+DC=2.7-1.5=1.2.
故答案为:4.2或1.2.
点评 本题考查了勾股定理,把三角形斜边转化到直角三角形中用勾股定理解答.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
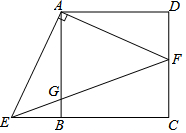 如图,在正方形ABCD中,F是CD边上的一点,AE⊥AF,AE交CB的延长线于点E,连接EF交AB于点G.
如图,在正方形ABCD中,F是CD边上的一点,AE⊥AF,AE交CB的延长线于点E,连接EF交AB于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
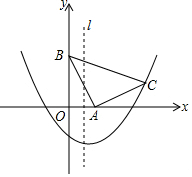 如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=$\frac{1}{2}$x2+bx-2的图象过C点.
如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=$\frac{1}{2}$x2+bx-2的图象过C点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a>b,则a+c>b+c | B. | 若a+c>b+c,则a>b | C. | 若a>b,则ac2>bc2 | D. | 若a>b,则1+a>b-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查白银市市民的吸烟情况 | |
| B. | 调查白银市电视台某节目的收视率 | |
| C. | 调查白银市市民家庭日常生活支出情况 | |
| D. | 调查白银市某校八年级二班学生对“文明白银”的知晓率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com