
分析 (1)由根与系数的关系可得出tanA•tanB=12k2-37k+26,根据正切的定义即可得出tanA•tanB=$\frac{a}{b}$•$\frac{b}{a}$=1,由此即可得出关于k的一元二次方程,解之即可得出k的值,将k值代入原方程再根据根的判别式△≥0即可确定k的值;
(2)将k的值代入原方程,解方程求出x的值,分a<b和a>b两种情况考虑,根据x的值结合c=10利用勾股定理即可求出a、b的值,此题得解.
解答 解:(1)∵tanA、tanB是关于x的一元二次方程x2-kx+12k2-37k+26=0的两个实数根,
∴tanA•tanB=12k2-37k+26.
又∵tanA•tanB=$\frac{a}{b}$•$\frac{b}{a}$=1,
∴12k2-37k+26=1,
解得:k1=$\frac{25}{12}$,k2=1.
当k2=1时,原方程化为x2-x+1=0,
此时△=(-1)2-4×1×1<0,不合题意,舍去,
∴k=$\frac{25}{12}$.
(2)当k=$\frac{25}{12}$时,原方程化为x2-$\frac{25}{12}$x+1=0,
解得:x1=$\frac{4}{3}$,x2=$\frac{3}{4}$.
①当a>b时,∴tanA=$\frac{a}{b}$=$\frac{4}{3}$,
不妨设a=4m,b=3m(m>0),
∴c=5m,
∵c=10,
∴5m=10,
∴m=2,
∴a=8,b=6;
②当a<b时,∴tanA=$\frac{a}{b}$=$\frac{3}{4}$,
同理可得a=6,b=8.
∴a=6,b=8或a=8,b=6.
点评 本题考查了根的判别式、根与系数的关系以及勾股定理,利用勾股定理求出三角形的两直角边长是解题的关键.


科目:初中数学 来源: 题型:解答题
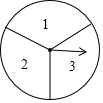 如图,一个转盘被分成3等分,每一份上各写有一个数字,随机转动转盘2次,第一次转到的数字数字为十位数字,第二次转到的数字为个位数字,2次转动后组成一个两位数(若指针停在等分线上则重新转一次)
如图,一个转盘被分成3等分,每一份上各写有一个数字,随机转动转盘2次,第一次转到的数字数字为十位数字,第二次转到的数字为个位数字,2次转动后组成一个两位数(若指针停在等分线上则重新转一次)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com