
 .在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.
.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.
 或﹣2
或﹣2 ≤t≤4.
≤t≤4. t,OO′=t,
t,OO′=t, t,NO′=
t,NO′= t,
t, t,
t, t),
t), ,
, ,
, x+
x+ t①,
t①, ,
, )),代入反比例函数的解析式得:k=4
)),代入反比例函数的解析式得:k=4 ,
, ②,
②, x2﹣
x2﹣ tx+4
tx+4 =0,
=0, t,
t, t)2﹣
t)2﹣ +4=0,
+4=0, t﹣
t﹣ t)2﹣
t)2﹣ +4=0,
+4=0, ,
, 或t≥﹣2
或t≥﹣2 ,
, 或﹣2
或﹣2 ≤t≤﹣4.
≤t≤﹣4.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源:不详 题型:解答题
 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE= .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 以加热的饮水机,该饮水机的工作程序是:放满水后,
以加热的饮水机,该饮水机的工作程序是:放满水后, 接通电源,则自动开始加热,每分钟水温上升10ºC,待加热到100ºC,饮水机自动切断电源,水温开始下降,水温和时间成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20ºC,接通电源后,水温和时间的关系下图所示,回答下列问题;
接通电源,则自动开始加热,每分钟水温上升10ºC,待加热到100ºC,饮水机自动切断电源,水温开始下降,水温和时间成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20ºC,接通电源后,水温和时间的关系下图所示,回答下列问题;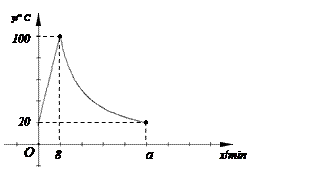 |
| 时间 | 节次 | |
| 上午 | 7:20 | 到校 |
| 7:45~8:20 | 第一节 | |
| 8:30~9:05 | 第二节 | |
| …… | …… | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com