
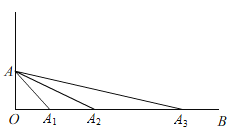
【题目】如图,已知∠AOB=90°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1,AA2,AA3…,依此作法,则∠AA2A3=___,∠AAnAn+1等于___度.(用含n的代数式表示,n为正整数).
【答案】157.5°, 180–![]() .
.
【解析】
根据旋转的性质得OA=OA1,则根据等腰三角形的性质得∠AA1O=![]() ,同理得到A1A=A1A2,根据等腰三角形的性质和三角形外角性质得到∠AA2A1=
,同理得到A1A=A1A2,根据等腰三角形的性质和三角形外角性质得到∠AA2A1=![]() ∠AA1O=
∠AA1O=![]() ,同样得到∠AA3A2=
,同样得到∠AA3A2=![]() ,于是可推广得到∠AAnAn-1=
,于是可推广得到∠AAnAn-1=![]() ,然后利用邻补角的定义得到∠AAnAn+1=180°-
,然后利用邻补角的定义得到∠AAnAn+1=180°-![]() .
.
∵点A绕点O顺时针旋转后的对应点A1落在射线OB上,
∴OA=OA1,
∴∠AA1O=![]() ,
,
∵点A绕点A1顺时针旋转后的对应点A2落在射线OB上,
∴A1A=A1A2,
∴∠AA2A1=![]() ∠AA1O=
∠AA1O=![]() ,
,
∴∠AA2A3=180°-∠AA2A1=157.5°
∵点A绕点A2顺时针旋转后的对应点A3落在射线OB上,
∴A2A=A2A3,
∴∠AA3A2=![]() ∠AA2A1=
∠AA2A1=![]() ,
,
∴∠AAnAn-1=![]() ,
,
∴∠AAnAn+1=180°-![]() .
.
故答案为:157.5°,180-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(1,﹣1),C(2,2),抛物线y=ax2(a≠0)经过△ABC区域(包括边界),则a的取值范围是( )
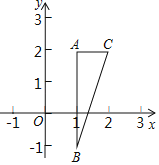
A.a≤﹣1或a≥2B.![]() ≤a≤2
≤a≤2
C.﹣1≤a<0或1<a≤![]() D.﹣1≤a<0或0<a≤2
D.﹣1≤a<0或0<a≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
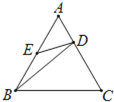
【题目】如图,在正三角形ABC中,点D、E分别在AC、AB上,且![]() ,AE=BE,则有( )
,AE=BE,则有( )
A.△AED∽△BEDB.△AED∽△CBD
C.△AED∽△ABDD.△BAD∽△BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
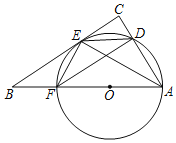
【题目】如图,AF为⊙O的直径,点B在AF的延长线上,BE切⊙O于点E,过点A作AC⊥BE,交BE的延长线交于点C,交⊙O交于点D,连接AE,EF,FD,DE.
(1)求证:EF=ED.
(2)求证:DFAF=2AEEF.
(3)若AE=4![]() ,DE=2
,DE=2![]() ,求sin∠DFA的值.
,求sin∠DFA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BC=2,AB=AC,点D为![]() 上的动点,且cos∠ABC=
上的动点,且cos∠ABC=![]() .
.
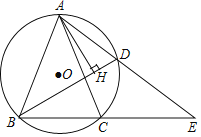
(1)求AB的长度;
(2)在点D的运动过程中,弦AD的延长线交BC延长线于点E,问ADAE的值是否变化?若不变,请求出ADAE的值;若变化,请说明理由;
(3)在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点O是AC边上的一个动点,过点O作直线
中,点O是AC边上的一个动点,过点O作直线![]() ,设MN交
,设MN交![]() 的角平分线于点E,交
的角平分线于点E,交![]() 的外角平分线于点F.
的外角平分线于点F.
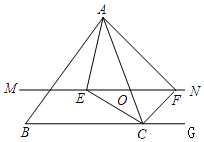
![]() 求证:
求证:![]() ;
;
![]() 当点O运动到何处时,四边形AECF是矩形?请说明理由;
当点O运动到何处时,四边形AECF是矩形?请说明理由;
![]() 在
在![]() 的条件下,给
的条件下,给![]() 再添加一个条件,使四边形AECF是正方形,那么添加的条件是______.
再添加一个条件,使四边形AECF是正方形,那么添加的条件是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.
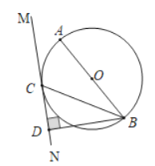
(1)求证:∠ABC=∠CBD;(2)若BC=4![]() ,CD=4,则⊙O的半径是 .
,CD=4,则⊙O的半径是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为( )
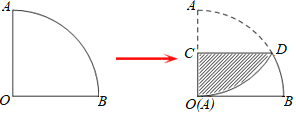
A. 6π﹣![]() B. 6π﹣9
B. 6π﹣9![]() C. 12π﹣
C. 12π﹣![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com