
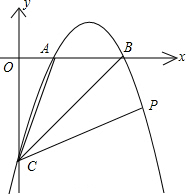
 如图,在直角坐标中,直线y=kx-3,分别与x轴,y轴交于B(3,0)、C,过B、C两点的抛物线y=ax2+bx+c与x轴交于另一点A(点A在B左边),且S△ABC=3
如图,在直角坐标中,直线y=kx-3,分别与x轴,y轴交于B(3,0)、C,过B、C两点的抛物线y=ax2+bx+c与x轴交于另一点A(点A在B左边),且S△ABC=3 AB•OC=
AB•OC= AB×3=3,
AB×3=3,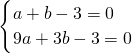 ,
, ,
, ,如图,延长CP交x轴于点Q,
,如图,延长CP交x轴于点Q,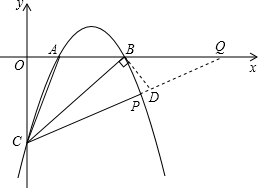 ,
,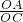 =
= ,AC=
,AC= ,
, ,
, ×3
×3 =
= ,
,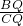 =
=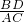 ,
,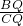 =
=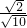 =
= ,
, n,
n, n)2,
n)2, (负值,舍去),n2=3,
(负值,舍去),n2=3, ,
, x-3,
x-3,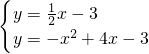 ,
,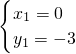 (为点C坐标,舍去),
(为点C坐标,舍去),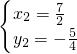 .
. ,-
,- ).
). ,延长CP交x轴于点Q,可以求出∠OCA=∠BCQ,然后求出∠BCQ的正切值,再过B点作BD⊥BC交CQ于点D,然后求出BD的长度,并判定△BQD和△CQA相似,设BQ=n,根据相似三角形对应边成比例用n表示出CQ,在Rt△OCQ中,根据勾股定理列式求出n的值,再求出OQ,从而得到点Q的坐标,然后根据待定系数法求出直线CQ解析式,在与抛物线解析式联立求解即可得到点P的坐标.
,延长CP交x轴于点Q,可以求出∠OCA=∠BCQ,然后求出∠BCQ的正切值,再过B点作BD⊥BC交CQ于点D,然后求出BD的长度,并判定△BQD和△CQA相似,设BQ=n,根据相似三角形对应边成比例用n表示出CQ,在Rt△OCQ中,根据勾股定理列式求出n的值,再求出OQ,从而得到点Q的坐标,然后根据待定系数法求出直线CQ解析式,在与抛物线解析式联立求解即可得到点P的坐标.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
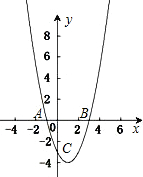 如图,在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与y轴的负半轴相交于点C,点C的坐标为(0,-3),且BO=CO.
如图,在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与y轴的负半轴相交于点C,点C的坐标为(0,-3),且BO=CO.查看答案和解析>>
科目:初中数学 来源: 题型:
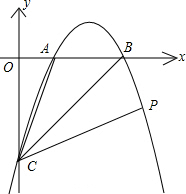 (2012•德化县一模)如图,在直角坐标中,直线y=kx-3,分别与x轴,y轴交于B(3,0)、C,过B、C两点的抛物线y=ax2+bx+c与x轴交于另一点A(点A在B左边),且S△ABC=3
(2012•德化县一模)如图,在直角坐标中,直线y=kx-3,分别与x轴,y轴交于B(3,0)、C,过B、C两点的抛物线y=ax2+bx+c与x轴交于另一点A(点A在B左边),且S△ABC=3查看答案和解析>>
科目:初中数学 来源:2012年福建省泉州市德化县中考数学一模试卷(解析版) 题型:解答题
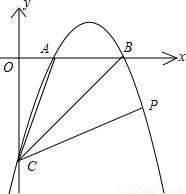
查看答案和解析>>
科目:初中数学 来源:2012年福建省泉州市德化县初中学业质量检查数学试卷(解析版) 题型:解答题
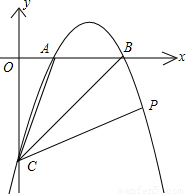
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com