
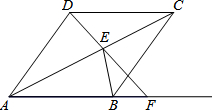
 如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连接DE并延长交射线AB于点F,连接BE.
如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连接DE并延长交射线AB于点F,连接BE.分析 (1)直接利用全等三角形的判定方法得出△DCE≌△BCE(SAS),即可得出答案;
(2)利用等腰三角形的性质结合垂直的定义得出∠DAB的度数;
(3)利用正方形的性质结合等腰三角形的性质得出①当F在AB延长线上时,以及②当F在线段AB上时,分别求出即可.
解答 (1)证明:∵四边形ABCD为菱形,
∴DC=CB,
在△DCE和△BCE中
$\left\{\begin{array}{l}{DC=CB}\\{∠DCE=∠BCE}\\{EC=EC}\end{array}\right.$,
∴△DCE≌△BCE(SAS),
∴∠EDC=∠EBC,
由DC∥AB得,∠EDC=∠AFD,
∴∠AFD=∠EBC;
(2)解:∵DE=EC,
∴∠EDC=∠ECD,
设∠EDC=∠ECD=∠CBE=x°,则∠CBF=2x°,
由BE⊥AF得:2x+x=90°,
解得:x=30°,
∴∠DAB=60°;
(3)分两种情况:
①如图1,当F在AB延长线上时,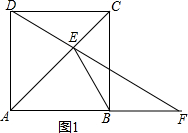
∵∠EBF为钝角,
∴只能是BE=BF,设∠BEF=∠BFE=x°,
可通过三角形内角形为180°得:
90+x+x+x=180,
解得:x=30,
∴∠EFB=30°;
②如图2,当F在线段AB上时,
∵∠EFB为钝角,
∴只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°,
可证得:∠AFD=∠FDC=∠CBE,
得x+2x=90,
解得:x=30,
∴∠EFB=120°,
综上:∠EFB=30°或120°.
点评 此题主要考查了菱形的性质以及正方形的性质以及全等三角形的判定与性质等知识,利用分类讨论得出是解题关键.


 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
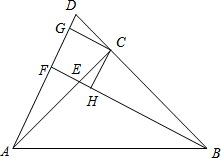 已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E在边AC上,延长BC至D点,使CE=CD,延长BE交AD于F,过点C作CG∥BF,交AD于点G,在BE上取一点H,使∠HCE=∠DCG.
已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E在边AC上,延长BC至D点,使CE=CD,延长BE交AD于F,过点C作CG∥BF,交AD于点G,在BE上取一点H,使∠HCE=∠DCG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛一枚硬币,正面朝上 | |
| B. | 黑暗中从5把不同的钥匙中随意摸出一把,用它打开了门 | |
| C. | 打开电视机,任选一个频道,屏幕上正在播放新闻联播 | |
| D. | 4个人分成3组,其中一组必有2人 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 摸球次数 | 10 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 出现红球的频数 | 4 | 9 | 16 | 31 | 44 | 61 | 74 | 92 | 118 | 147 |
| 出现白球的频数 | 1 | 4 | 16 | 36 | 52 | 61 | 75 | 85 | 123 | 151 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了了解某中学800名学生的视力情况,从中随机抽取了50名学生进行调查,在此次调查中,样本容量为50名学生的视力 | |
| B. | 若一个游戏的中奖率是1%,则做100次这样的游戏一定会中奖 | |
| C. | 了解无锡市每天的流动人口数,采用抽查方式 | |
| D. | “掷一枚硬币,正面朝上”是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com