
分析 利用一次函数图象上点的坐标特征可求出点P、Q的坐标,根据P、Q点关于x轴对称可得出关于m的一元二次方程,解之即可得出m的值,再利用一次函数的定义可确定m的值,此题得解.
解答 解:当x=0时,y=(m2-4)x+(1-m)=1-m,
∴点P的坐标为(0,1-m);
当x=0时,y=(m+2)x+(m2-3)=m2-3,
∴点Q的坐标为(0,m2-3).
∵P、Q点关于x轴对称,
∴-(1-m)=m2-3,即m2-m-2=0,
解得:m=-1或m=2.
又∵m2-4≠0,m+2≠0,
∴m≠±2,
∴m=-1.
故答案为:-1.
点评 本题考查了一次函数图象上点的坐标特征、关于x轴、y轴对称的点的坐标以及一次函数的定义,利用一次函数图象上点的坐标特征求出点P、Q的坐标是解题的关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
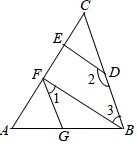 如图,DE⊥AC,∠AGF=ABC,∠1+∠2=180°,
如图,DE⊥AC,∠AGF=ABC,∠1+∠2=180°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图 A(0,-4)、B(-2,0),M为直线l1:x=-1上一点,N为直线l2:y=x+3上一点.若以A、B、M、N为顶点的四边形是平行四边形,求所有满足条件的点N的坐标;
如图 A(0,-4)、B(-2,0),M为直线l1:x=-1上一点,N为直线l2:y=x+3上一点.若以A、B、M、N为顶点的四边形是平行四边形,求所有满足条件的点N的坐标;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
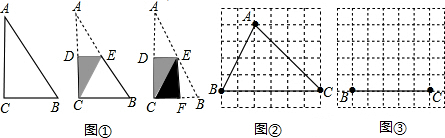
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 端午节是我国四大传统文化节日之一,为每年的农历五月初五,自古以来端午节便有划龙舟及食粽等习俗.重庆某大型超市为了了解市民对“蛋黄粽”的喜好程度,特意在三峡广场做了试吃及问卷调查活动,将市民对“蛋黄粽”的喜好程度分为“A非常喜欢”、“B比较喜欢”、“C感觉一般”、“D不太喜欢”四个等级,并将四个等级分别计分为:A等级10分,B等级7分,C等级5分,D等级2分,根据调查结果绘制出如图所示的条形统计图,请问“蛋黄粽”的平均分是7分.
端午节是我国四大传统文化节日之一,为每年的农历五月初五,自古以来端午节便有划龙舟及食粽等习俗.重庆某大型超市为了了解市民对“蛋黄粽”的喜好程度,特意在三峡广场做了试吃及问卷调查活动,将市民对“蛋黄粽”的喜好程度分为“A非常喜欢”、“B比较喜欢”、“C感觉一般”、“D不太喜欢”四个等级,并将四个等级分别计分为:A等级10分,B等级7分,C等级5分,D等级2分,根据调查结果绘制出如图所示的条形统计图,请问“蛋黄粽”的平均分是7分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com