
【题目】正方形ABCD中,E、F分别在AD、DC上,∠ABE=∠CBF=15°,G是AD上另一点,且∠BGD=120°,连接EF、BG、FG、EF、BG交于点H,则下面结论:①DE=DF;②△BEF是等边三角形;③∠BGF=45°;④BG=EG+FG中,正确的是(请填番号) 
【答案】①②④
【解析】证明:连接BD,在BG上取一点M,使得GM=GF. ∵四边形ABCD是正方形,
∴AB=CB=AD=CD,∠ABC=∠A=∠C=90°,∠ABD=∠CBD=45°,
在△BAE和△BCF中,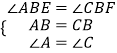 ,
,
∴△BAE≌△BCF,
∴BE=BF,AE=CF,
∴DE=DF,故①正确,
∵∠ABE=∠CBF=15°,
∠EBF=60°,
∴△EBF是等边三角形,故②正确,
∵∠BGD=120°,
∴∠EGH=∠HFB=60°,
∵∠EHG=∠BHF,
∴△EHG∽△BHF,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠EHB=∠GHF,
,∵∠EHB=∠GHF,
∴△EHB∽△GHF,
∴∠BEH=∠BGF=60°,故③错误,
∵GM=GF,
∴△GMF是等边三角形,
∴FM=FG,∠MFG=∠BFE=60°,
∴∠BFM=∠EFG,∵BF=FE,
∴△BFM≌△EFG,
∴BM=EG,
∴GB=GM+BM=GF+EG,故④正确.
所以答案是①②④.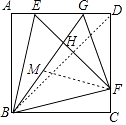
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


科目:初中数学 来源: 题型:
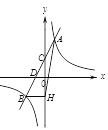
【题目】一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象相交于A、B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2,过点B作BH⊥y轴于点H,连接 AH.
(k≠0)的图象相交于A、B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2,过点B作BH⊥y轴于点H,连接 AH.
(1)求一次函数和反比例函数的解析式;(2)求△ABH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
(1)求该抛物线的解析式;
(2)若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;
(3)该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,△ABC中,∠BAC=90°,AB=AC,分别过点B、C作经过点A的直线L的垂线段BD、CE,垂足分别D、E. 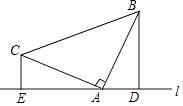
(1)求证:DE=BD+CE.
(2)如果过点A的直线经过∠BAC的内部,那么上述结论还成立吗?请给出你的结论,并画出图形予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A、B),过B、C、E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.
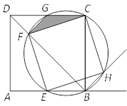
(1)求证:四边形EFCH是正方形;
(2)设BE=x,△CFG的面积为y,求y与x的函数关系式,并求y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
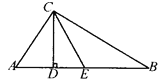
【题目】已知:如图,在△ABC中,∠ACB=90°,CD为高,CE平分∠BCD,且∠ACD:∠BCD=1:2,那么CE是AB边上的中线对吗?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com