
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A,B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②![]() ;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
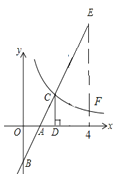
A. 1 B. 2 C. 3 D. 4
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )

A. (1,﹣1) B. (2,0) C. (﹣1,1) D. (﹣1,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
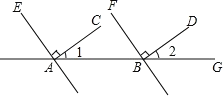
【题目】如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以___∥___( ).
又因为AC⊥AE(已知),所以∠EAC=90°( )
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=__ °.
所以∠EAB=∠FBG( ).
所以___∥___(同位角相等,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
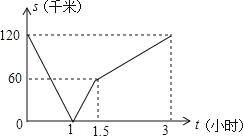
【题目】一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
①A、B两地相距60千米;
②出发1小时,货车与小汽车相遇;
③小汽车的速度是货车速度的2倍;
④出发1.5小时,小汽车比货车多行驶了60千米.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线l1:y=2x+8与坐标轴分别交于A,B两点,点C在x正半轴上,且OA=OC.点P为线段AC(不含端点)上一动点,将线段OP绕点O逆时针旋转90°,得线段OQ(见图2)
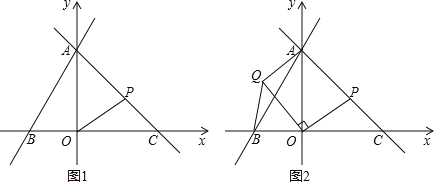
(1)分别求出点B、点C的坐标;
(2)如图2,连接AQ,求证:∠OAQ=45°;
(3)如图2,连接BQ,试求出当线段BQ取得最小值时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
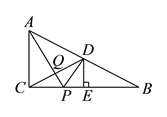
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 是
是![]() 边的中点,过
边的中点,过![]() 作
作![]() 于点
于点![]() ,点
,点![]() 是边
是边![]() 上的一个动点,
上的一个动点, ![]() 与
与![]() 相交于点
相交于点![]() .当
.当![]() 的值最小时,
的值最小时, ![]() 与
与![]() 之间的数量关系是__________.
之间的数量关系是__________.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017怀化,第10题,4分)如图,A,B两点在反比例函数![]() 的图象上,C,D两点在反比例函数
的图象上,C,D两点在反比例函数![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则![]() 的值是( )
的值是( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.

(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的![]() ;
;
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对即将参加中考的4000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

(1)本次调查样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com